Gender conservatism among young people

Back in February, New York Times writer Clair Cain Miller wrote a piece about recent research on the gendered division of labor among heterosexual partners.   Part of her article discussed the study by sociologists Brittany Dernberger and Joanna Pepin, who used Monitoring the Future data to track 12th-graders’ attitudes towards division of labor arrangements from 1976 to 2014.  These students were asked to imagine being married and having at least one preschool-aged child.  They were asked to indicate the desirability of various division of labor schemes (e.g. “husband works full time, wife doesn’t work” or “husband workers about half time, wife works full time”; the only permutation of working full-time/working half-time/not working not asked was both husband and wife not working).  They found that while the desirability of the traditional breadwinner-husband/stay-at-home wife scheme had declined since the 1970, it was still the most desireable arrangement in 2014.  In 1976, 44 percent of students thought the traditional arrangement was “desireable” (as opposed to “acceptable” or “not at all acceptable”); in 2014 this was down to 23 percent.  But people desiring gender parity (saying that both working part-time or both working full-time were desireable) had risen only slightly, from 9 percent to 19 percent.

 

Figure 1 in Dernberger & Peppin (2020), p. 43

For my general education statistics class, an early assignment I have my students do is double-check a media write-up of results so they go from the media piece, to the study, and then they go and look into the actual data documents (like questionnaires).  In this case, it looks like Miller’s write-up checks out.  It was a little bit of a struggle to get the MTF questionnaires or codebooks but ICPSR has them; in the case of 2014, the questions about imaginary division of labor arrangements is in “Form 2”.

 

Long-lasting symptoms of COVID

Fabio Rojas has argued for most institutions reopening in the face of COVID-19, on the grounds that COVID mortality rates are quite low for the non-elderly.

A number of commenters on his posted legitimately raised the issue of people with serious, long-lasting complications from COVID.  It’s just not a matter of a few people dying and the overwhelming majority of people recovering, but we are hearing about people who have been suffering for months from debilitating, COVID-related complications.

This raises the question, how common are these so-called COVID-19 “long-haulers”?

The CDC released a study a last week tracing the resolution of COVID-19 among people with mild symptoms–that is, who were diagnosed in out-patient clinics (rather than being diagnosed having been hospitalized for serious COVID-19 symptoms).  Some media accounts [1,2,3] are linking the study to the nightmarish long-hauler phenomenon, but I am skeptical.

The CDC obtained a list of people testing positive between March 31 and June 4 from 14 academic health centers and they randomly sampled individuals within each test site.  Subjects were called 2-3 weeks after their test date and interviewed about their symptoms.  They were able to interview around 46% of their sample (274/582).

Among these interviewees, 35 percent said they had not returned to usual health  at the time of the interview, with the rate depending on age (at most a third of those less than 50 years old still had symptoms; around half of those 50 years or older still reported dealing with symptoms).  The most common symptoms failing to resolve were coughing and fatigue (43 and 35 percent of people experiencing those respective symptoms on the day of testing reported still having them at the day of the interview); fevers  and chills resolved for nearly everyone experiencing those symptoms on the day of testing.

[a CNN report on this study misreported the symptom results as “for the people whose symptoms lingered, 43% said they had a cough, 35% said they felt tired…” which implies that 15% of subjects still had a cough (that is, 43% of the 35% who still felt unwell at the time of the interview).   In reality, it was 26% of subjects still reporting having a cough–that is 43% of the 166 subjects reporting having a cough at the time of testing.]

It is not clear to me how serious these symptoms are; it looks like many people who had mild cases of COVID-19 were still impaired for 2-3 weeks, but I thought we already knew that having COVID-19 could mean being sick for a couple of weeks.  I wish the CDC had interviewed people a bit further out from the time of a positive test result (as long-haulers say they have been sick for months).  In addition, the CDC is not making the survey instrument available but the measurement of symptoms seems binary and does not capture the debilitating nature of the long-hauler symptoms.

I would also guess that the study’s estimates of the prevalence of long-lasting symptoms are upwardly biased, as people with mild forms of COVID-19 are probably (a) less likely to get tested and (b) less likely to have enduring symptoms.  I suspect, but I don’t really know, that people with long-lasting symptoms are also more likely to agree to an interview request from health researchers (although if they are really sick they may not; the researchers excluded nine subjects because a proxy did the interview and I wonder if that was because they felt too unwell to talk with an interviewer).

Having said that, I do not endorse arguments for re-opening, or even qualified ones calling for re-opening for the non-elderly while keeping the elderly locked down (I am not even sure what that would look like, much less work).  While I suspect long-hauler cases are rare, we just do not know enough about the disease to let it burn through the population (even the non-elderly population).

Oh PISA

Trying not to go for something obvious here

In Damned Lies and Statistics, Joel Best argues that consumers of statistics need to especially scrutinize international comparisons because there are so many opportunities to mix up apples and oranges (I have discussed this with regard to the conceptual definitions used to quantify police-related deaths in different countries).   One of Best’s examples was international comparisons of test scores; he pointed out that sampling strategies used vary across countries and often countries’ performance levels could be chalked up to the broadness of their sampling strategy.  In particular, countries with comprehensive secondary school systems (like the United States, where all, or nearly all, adolescents are exposed to an academic-focused curriculum) would sample from the entire population of schools, while countries with  “streaming” systems (like in Germany), where some adolescents go to academic high schools while others go to more vocationally-oriented schools, would sample from the academic high schools only.  This would stack the deck against countries like the United States.

Damned Lies and Statistics came out in 2001, and the international testing comparisons Best talked about have been supplanted by the Programme for International Student Achievement (PISA), run by the OECD.  When I teach Best in my statistics class, I show students the general sampling strategy of PISA:

The desired base PISA target population in each country consisted of 15-year-old students attending educational institutions located within the country. This meant that countries were to include (i) 15-year-olds enrolled full-time in educational institutions, (ii) 15-year-olds enrolled in educational institutions who attended on only a part-time basis, (iii) students in vocational training types of programmes, or any other related type of educational programmes…

Sure, there were some problems with China, but what you are going to do?  Surely PISA must be good for comparing democratic countries, right?

Well, no.  A team of UCL educational researchers headed by Jake Anders have analyzed the 2015 Canadian sample for PISA and their analysis raises questions about the quality of comparisons involving Canada, which does very well on the PISA in terms of high average scores.

Their article is nice for walking the reader through the sampling strategy of PISA countries.

  • First you have to talk about sample exclusions–what part of the population are you trying to generalize to, and what part are you not trying to generalize to?  As shown above, PISA is trying to get at 15-year olds in any kind of educational institution.  In Canada, that covers 96 percent of 15-year olds so you are dropping 4 percent right off the bat there (the Anders article has a really nice table comparing Canada’s figures to other countries including the United States, where 95% of 15-year-olds are in educational institutions).
  • Not mentioned above is that PISA lets countries exclude students from their target population based on Special Needs (although PISA caps this at 5% of students).  In 2015 Canada broached this cap–Anders et al. note that Canada “has one of the highest rates of student exclusions (7.5%).” So now Canada’s sample is supposed to cover 88.8 [96%*(1-.075)] percent of Canadian 15-year olds.
  • PISA countries are in charge of their own sampling, and I did not realize how much discretion they have.  With nationally representative samples, you really need to do stratified sampling (and probably clustered sampling as well which Anders et al do not get into).  Stratified sampling means countries divide schools into strata based on combinations of variables and sample from each of their strata to ensure a representative sample.  Countries choose their own stratifying variables (!), and in Canada these are “province, language, and school size” which seems fine to me.
  • We have not even talked about school and student non-compliance, and here is where things get really messy.  Canada selected 1008 schools to participate in the 2015 PISA, and 30% refused.  What countries can do is try to recruit “replacement schools” that are similar to refusing schools based on the stratifying variables as well as another set of variables (which Anders et al. refer to as “implicit” stratifying variables).  Canada was able to recruit 23 replacement schools, but it is not clear that the variables Canada used to implicitly stratify schools were that meaningful for test scores–meaning it is possible that the replacement schools are very different from the originally-selected schools in unobserved ways.  It is only 2% of the sample but this problem of using meaningless variables to gauge the representativeness of the sample will be an issue.
  • Anders et al. points out that at 70%, Canada is fourth-worst among OECD countries in terms of the response rate of initial schools (beaten out by the Netherlands, New Zealand, and USA).  In terms of overall response rate (after including the replacement schools) Canada’s 72 is the worst (the US, at 83 percent, still looks very bad relative to other OECD countries, most of which are at 95 percent or above).
  • PISA requires countries with low initial response rates between 65% and 85% to do a non-response bias analysis (NRBA).  Countries below 65% (like the Netherlands) are supposed to be excluded, but in this case, they were not.  PISA does not report the details of these NRBAs, and Anders et al.  tracked down Canada’s province-specific NRBAs and found they were pretty superficial, and suffered from the problem of using a handful of variables to show that non-responding schools are similar to responding schools (although in the case of Quebec there were significant differences between refusal and complying schools).
  • Now we get into pupil non-response, and again, Canada is among the worse in this regard, with 81% of students in complying schools taking the PISA tests (the other two countries with worse or comparable rates are Austria at 71% and Australia also at 81%).  We know that non-participating students tend to do worse on the tests, and one way to get around this is to weigh student participants such that those with characteristics similar to non-participants are weighted more.  But again, we get into this issue where Canada uses weights based on variables that do not really matter for test scores (the stratifying variables plus “urbanisation, source of school funding, and [school level]”).
  • I am not sure how Anders et al. calculate this, but all told, Canada’s sample is really only representative of 53% of Canadian students (although I wonder if they meant to say 53% of Canadian 15-year olds).
  • Anders et al. do some simulations for reading scores, assuming that non-participant students on average would perform worse on the PISA tests than participant students.  If we assume that the non-participating students do moderately worse on the PISA instrument (say, at the 40 or 35th percentiles), Canada’s reading scores are still better than average but are not at the “super-star” levels it enjoys with its reported performance.  If we assume the non-participants do substantially worse (say, at the 30th percentile) for Canada’s mean PISA reading scores take a serious dive and Canada starts looking more like an average country.

The one thing that really sticks out here–and also with Tom Loveless’s discussion of PISA and China–is that PISA’s behavior is not consistent with the dispassionate collection and analysis of data.  They have opened the door to countries (especially wealthy ones) fudging their data and they do not really seem to care.

On Judicial Watch’s figures…

Last week I went down the rabbit hole of looking up the study by Jesse Richman and colleagues purporting to quantify the extent of voting among non-citizens in the United States in the 2008 and 2010 elections.  I and other people have very serious concerns about their analyses.  But setting that aside I was very curious about the “estimate” that Tom Fitton gave in this Judicial Watch video about the number of non-citizens voting in the 2016 and 2018 elections:

I’ve calculated, because there’s this study, I don’t know if you’ve seen it, Bruce, out of Old Dominion University, we’ve talked about it extensively here at Judicial Watch.  And it’s a numbers game.  You’ve got XX million numbers of illegal aliens and just aliens who are here lawfully, they have green cards, and a percentage of them are going to register to vote, both in a knowingly criminal way, and accidentally.  And of those, a percentage are going to vote.   And they vote in large enough numbers to influence elections.  It makes sense.  And when you look at the numbers from the study you extrapolate them for instance to 2016, I’d estimate about 1.2 million aliens voted in the presidential election…you look at them in 2018, those numbers, given the turnout, I’d estimate you had 900,000 aliens unlawfully vote in the mid-term elections.  

Now, I want to be very clear here, extrapolation is very fraught, and especially so in this context.  I have expressed my deep skepticism that the number of non-citizen voters is above “negligible” on the grounds that voting is irrational for citizens in a pure cost-benefit analysis (because your one vote very unlikely to to sway an election), and it is especially irrational for non-citizens, who face even more costs in terms of being caught voting illegally.  Even if we give credence to Richman et al.’s estimates of the prevalence of non-citizen voting (and I don’t), we have good reason to believe that, given the vigorous anti-immigration policies pursued by the Trump administration, non-citizen propensity to vote went down for the 2018 midterm out of fear of being caught.

But again, let’s just set these serious reservations aside and see how the calculations turn out.

Richman et al.’s “best estimate” for the percentage of non-citizens voting in the 2008 and 2010 elections are 6.4 and 2.2, respectively.  We could assume that 6.4 percent of non-citizens vote in presidential elections and that 2.2 percent of non-citizens vote in mid-term elections and these turnout rates are constant.  We could apply those percentages to the number of adult non-citizens  living in the United States in the late 2010s (20,431,595) to estimate the counts of non-citizens voting in 2016 and 2018 and we would get 1.31 million votes in 2016 and 450,000 votes in 2018.  So Fitten is in the ballpark for 2016 but pretty far off for 2018.

Now, as Fitton said, turnout differs from year to year.  So instead of assuming that non-citizen voting turnout is fixed in presidential and mid-term elections, we could instead assume that the share of votes from non-citizens is fixed.  For presidential elections, that would be 1% of votes (based on the 2008 numbers; 1,260,606/131,313,820) and for midterm elections  that would be 1.5% of votes (based on the 2010 numbers; 440,315/87,134,148).  In 2016, that 1% would translate into 1.37 million votes (136,669,276*.01) and in 2018 that 1.5% would translate into 580,000 votes.

I don’t really know what Fitten did to get his extrapolations.  This is definitely a case of “garbage in, garbage out”, but to the extent you want the second-best handling of the garbage (the first being to ditch it altogether), I think my extrapolations do the job, and by this reckoning, Fitton is underestimating the turnout in 2016 by .17 million (or 12%) and over-estimating the turnout in 2018 by around .32 million (or 36%).   I put in a query to Judicial Watch and we’ll see if they answer (I kind of doubt it).

Non-Citizen Voting Revisited

A couple of days ago I wrote about a six-year old statistical controversy in political science (in my defense, it was new to me!), where Jesse Richman and his collaboraters used a massive online survey–the Cooperative Congressional Election Study (CCES)–to argue that non-citizen voting in the 2008 and 2010 elections in the United States was non-trivial.

Ansolabehere et al. Reply

The CCES principal investigators, led by Stephen Ansolabehere, wrote a reply.  They were able to investigate measurement error in the citizenship status variable in the 2010 data since respondents were followed-up in the 2012 wave.  They show that a non-trivial number of people who said they were non-citizens in 2010 indicated they were citizens in 2012 (36/121), which is not a big deal as they may have naturalized.  But, a non-trivial number of people who said they were non-citizens in 2012 indicated they were citizens in 2010 (20/105) which is  really worrisome; people losing their citizenship while still living in the United States is probably quite rare.  Ansolabehere et al. argue that these individuals are assuredly citizens who happened to misreport their citizenship in 2012.

It gets even worse for Richman et al.  Among the respondents whom we are confident are really non-citizens, since they consistently reported their status in 2010 and 2012, none reported voting in 2010.  Among the 141 respondents who indicated they were non-citizens in either the 2010 or 2012 waves, only four of them were validated as voting in 2010, and all four inconsistently reported their citizenship status.   Three were the assuredly fake “non-citizens” (who initially self-reported as a citizen in 2010 and then switched to self-reporting as a non-citizen in 2012).  The other  “non-citizen” whose 2010 voting participation was validated, said they were a non-citizen in 2010 and then said they were a citizen in 2012.  Although it is possible this person illegally voted as a non-citizen in 2010 and then naturalized by 2012, Ansolabehere et al. infer it is much more likely they were actually a true citizen in 2010.

Richman et al. Rejoinder

Richman and his colleagues have a response (which was written three years ago and is apparently not going to see print). First, they take issue with Ansolabehere et al.’s overstated conclusion that non-citizen voting is zero and complain about Ansolabehere’s lack of power with the 85 individuals who consistently self-reported as non-citizen in 2010 and 2012.

Second, Richman push back on the idea that non-citizens who have validated votes are really just citizens missclassified–they look at immigration attitudes in the 2012 CCES and show that the 32 non-citizen validated voters are quite similar to the 263 non-citizen validated non-voters, and both groups are quite different from citizens.

[A major argument Richman et al. make that I am glossing over is about Ansolabehere et al.’s estimate of the reliability of the citizenship status variable. Ansolabehere et al. assume that non-citizens and citizens are equally likely to misstate their status.  Since citizens are a much bigger group than non-citizens, a person with an inconsistent status is much, much more likely to truly be a citizen than a non-citizen.  Richman et al. argue that non-citizens are probably more likely to misstate their citizenship status, although this argument seems premised on the idea that voter fraud is widespread among non-citizens which I don’t think Richman et al. has established.  I think that if you buy Richman et al.’s argument, then the implication is if one looks at people with inconsistent citizenship statuses–namely those initially self-reporting as citizens in one wave and self-reporting as a non-citizen in the next wave–half are true citizens and half are true non-citizens].

Third, Richman et al. look at voter registration and find among respondents who were consistent self-reported non-citizens in 2010 and 2012, 5 out of 47 (10.6%) had validated voter registrations in 2012 and 1 out of 47 (2.1%) were validated voters in 2012; among respondents who were consistent self-reported non-citizens in 2010, 2012, and 2014, 1 out of 16 (6.3) had validated voter registrations in 2014 and 0 were validated voters in 2014.

My take

I have a couple of comments about this debate.

First, as someone who has zero exposure to the CCES data, I was frustrated by both sides in not clearly explaining why they were examining some waves and variables but not others.  For example, I was wondering why Ansolabehere et al. did not look at validated voting in the 2012 wave (as Richman et al. did in his rejoinder).  One does wonder about the issue of cherry-picking.

Second, in my previous blog post I expressed frustration with the original Richman et al. article because it was not clearly conveying its analyses, and I especially felt this way with the Richman et al. rejoinder.  Apparently, I am not the only one who has this reaction to Richman’s arguments.

Third, in the original Richman et al. piece, 27 and 13 so-called non-citizens reported they voted in the 2008 and 2010 elections, respectively.  Richman et al. use these quite small samples to estimate levels of Democratic voting nationwide among  non-citizen voters, and then assume these generalizations applied to non-citizen voters in specific contests (e.g. Minnesota in 2008).  They did not ever acknowledge sampling variability in this estimate.  In their rejoinder to Ansolabehere et al., they make a cheeky comment about how they were forced by Ansolabehere et al. to engage in analyses of small analyses: “If their critique, based as it is on such small samples, has any validity, then our response mu[st] join it on this terrain” (p. 10).  In reality, Richman et al. were the first to bring us to this terrain and for them to criticize Ansolabehere et al. for power issues seems like a case of the pot calling the kettle black.

Fourth, the comparison of 2012 immigrant attitudes of non-citizen voters, non-citizen non-voters, and citizens was probably the best evidence in favor of Richman et al.’s point of view (although I wish they broke out the citizens into voters and non-voters to have clearer comparisons).  I wonder why they  did not carry out such analyzes in the 2010 data–their original article actually used the 2010 data on immigration attitudes, but without a citizen/non-citizen voter/non-citizen non-voter comparison.

Fifth, I have to reiterate the point of my original blog post.  Richman et al. want to chalk up measurement error in the citizenship variable to non-citizens wanting to cover up their illegal participation in the U.S. electoral system.  It just raises issues about the generalizability of the CCES sample of non-citizens to the population of non-citizens in the U.S.  If a non-citizen has illegally participated in the electoral system, and they feel compelled to have to lie about their citizenship status on a survey, why are they even participating in a survey about voting behaviors in the first place?  My point is not to deny it has ever happened–I am sure it must have–but that the people doing this must be pretty unusual.  Richman et al. made a case that non-citizen voting was largely driven by ignorance as education did not predict non-citizen voting as it does for citizen voting.  A very logical inference is that the CCES is drawing on a select group of non-citizens combining high levels of ignorance and political interest, and again my suspicion is that the sample is systematically overestimating non-citizen voting.

 

 

 

 

 

 

Non-Citizen Voting in the United States

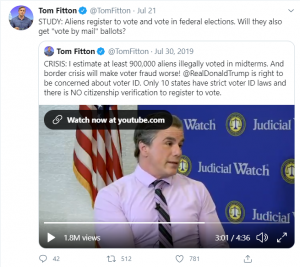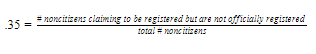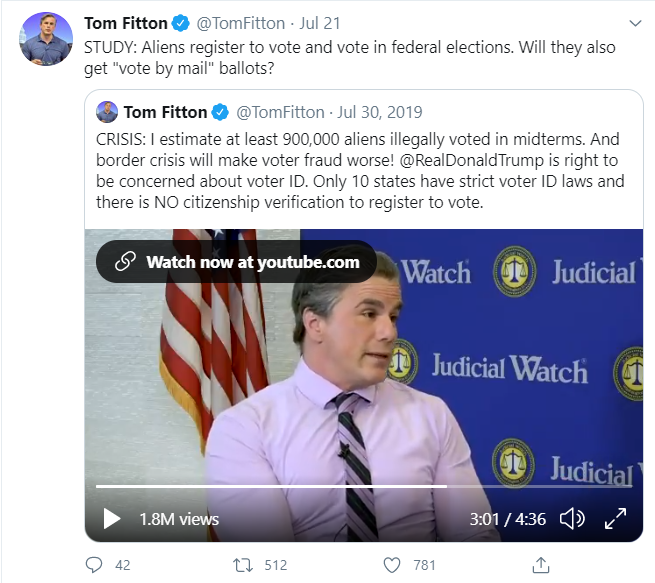
I saw this tweet by the president of the right-wing thinktank Judicial Watch and I was curious how he arrived at those numbers.  In the video he cites a 2014  study by Jesse Richman and colleagues purporting to quantify the extent to which non-citizens voted in the United States, which is nearly illegal everywhere in the country (except some localities in Maryland).  In this post I just want to address the Richman study (although I realize I am a latecomer to this study); how Fitton used its findings may be gristle for another post.

The Richman study

Richman et al. use the 2008 and 2010 waves of the Cooperative Congressional Election Study (CCES).  This is an online survey done by YouGov and respondents are sampled from YouGov’s panels.  Essentially, people volunteer to be on-going survey takers for YouGov and they provide demographic information to the company.  So when a client approaches YouGov–say, the consortium of political scientists who want to study voters in congressional elections–they can tell YouGov that they want a cross-section of American adult citizens.  In this case, the CCES team turned to existing data on U.S. citizens and figured out what a representative sample of U.S. voting-aged citizens would look like in terms of gender, age, race, region,  education, interest in politics, marital status, party identity, ideology, religion, church attendance, income, voter registration status, and urbanicity.  YouGov used this information to sample people from their panel to provide a “representative” sample of adult citizens.  When the data are actually being analyzed, researchers can use weights to make sure that certain categories or combinations of individuals are not overrepresented.

As luck would have it, despite trying to get a representative sample of U.S. voting-aged citizens, the CCES scooped up a couple of hundred of non-citizens in both the 2008 and 2010 waves so Richman et al. studied them.

Besides using an online survey, the virtue of the 2008 CCES is that it used official records to verify respondents’ voter registration and voter participation.

Richman et al. find that around 15% of the noncitizens in the 2008 CCES and 2010 CCES say they are registered to vote. From the subsample of the 2008 CCES where the researchers were able to link respondents to official voting records, Richman et al. find that of the noncitizens who said they were registered, only 65% actually were registered, and of the noncitizens who said they were not registered, 18% actually were.  So they infer that in both 2008 and 2010, 25% of non-citizens were registered to vote (15*.65 + 85*.18).

As an aside, the authors’ writing could have been clearer.  They authors throw around different sample sizes (it was not clear to me what was the size of the sample linked to official records–94 or 140) and I could not figure out the actual tabulations they used to get the 65% and 18% figures.  To be clear, I am not accusing them of finagling the analyses, just sloppy writing.  They also wrote up these conditional percentages in a very confusing way :

…our best guess at the true percentage of non-citizens registered…uses the 94 (weighted) non-citizens…match[ed] to commercial and/or voter databases to estimate the portion of non-citizens who either claim to be registered when they are not (35%) or claim not to be registered when they are (18%). [pp. 151-152]

It is not obvious what exactly the 35% and 18% figures are–that is, what exactly the denominator is.  Taking the 35% figure for instance, is it this:

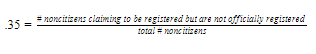
(no!)

or this?

(no!)

Or this?

(yes!)

As far as voting goes, in 2008, 27 non-citizen respondents (8%) reported they voted, and in 2010, 13 (3%) reported they voted.  Using similar math that I laid out above, Richman et al. estimate that in 2008, 6% of non-citizens voted, and in 2010, 2% voted.  Richman look at the political preferences of these very small samples and concluded that non-citizen voters lean heavily Democratic.  Based onthese nation-wide estimates of non-citizen voting and non-citizen voter political preferences and location-specific estimates of non-citizen residents, they conclude that non-citizen voters may have thrown elections in certain contests (namely, Obama’s victory in North Carolina in 2008 and Al Franken’s Senate victory in Minnesota in 2008).

Richman et al. find that unlike for the general population, the highly-educated are not more likely to vote.  Indeed, among non-citizens, the association is negative, from which they conclude that non-citizen voting is mostly accidental and done out of ignorance that it is illegal.

The Richman Study — what can we say about noncitizen voting?

It is tempting to dismiss the CCES data on the grounds that while the respondents may be demographically representative of the broader population, some unmeasured characteristics might set them apart from other people.  For instance, people who like taking surveys and join online survey panels just might be …weird.  In reality, the best online polls have a track record that is comparable to more traditional phone polling.  The Pew Research Center has shown this is the case specifically for looking at voter registration, and the documentation for the 2008 CCES provides evidence of YouGov’s impressive track record for previous surveys–in particular, I am struck by the 2006 CCES’s lack of bias in predicting state-wide elections.  So just because it is online does not mean we can just throw out the data.

Having said that, I think there are real questions to be asked about how representative the sample of noncitizens are in the CCES, especially since the CCES team asked YouGov to draw a sample representative of adult U.S. citizens.  Indeed, according to Richman et al., only 1% of the 2008 and 2010 CCES respondents reported being non-citizens.  In reality, Census data indicate that in the late 2000s, non-citizens made up 8 percent of voting-age adults in the United States.

Richman et al. acknowledge this issue, somewhat.  They note (p. 151) that their sample of non-citizen adults is much better educated than the population of non-citizen adults, and their fix for this issue to use sample weights (essentially weigh the highly-educated non-citizens less and weigh the less-educated non-citizens more).  But this assumes that selection into the CCES is driven only by the observed factors that are the basis of the weights, like education.  So if you correct for the education imbalance, then you can generalize to the rest of non-citizen voting-aged adults, right?

That seems to me an awfully heroic assumption.  I would guess that the non-citizens who select into the CCES study are an unusual group, composed of people interested in domestic politics but are either (a) unaware that political researchers are not interested in them because they can’t vote or (b) unaware they should not be voting.  My hunch is that the CCES sample is reflecting a small segment of the non-citizen population predisposed to vote.  I find it very unlikely that 25% of non-citizens were registered to vote in the late 2000s, or that 6% voted in the 2008 presidential election.  In other words, my hunch is that Richman et al. are using a biased sample.  When I say biased, I mean, in the sense that if you replicated the sampling methodology over and over, you would consistently over-estimate non-citizen voter registration and voter participation.

Richman et al. argue that the bias could go the other way–that non-citizens voters savvy enough to know they are committing a crime are going to be underrepresented in the data.  But how common is such a person?  Social scientists have talked about how voting is irrational even for citizens.  How much more irrational would it be to vote if it means committing crime and/or being deported from a country one presumably wants to stay in?

I am also really, really, not crazy about generalizing from the really small samples of self-confessed non-citizen voters to (a) non-citizens as a whole, and (b) applying those generalizations to non-citizen voters in particular contests, which just assumes that the distribution of political views among non-citizens is invariant across different contexts.

I wrote this post “fresh”–that is, without looking at what others had written about the study.  Maggie Koerth at fivethirtyeight.com wrote an article in 2017 nicely summarizing the subsequent dust-up (including a sympathetic look at one of Richman’s co-authors, who was an undergraduate student when she worked on the paper).    Richman et al.’s study has apparently been racked over the coals, with the CCES principal investigators chalking up Richman et al.’s findings to measurement error for citizenship status (although why the CCES PIs used the 2010/2012 CCES instead of the 2008/2010 CCES baffles me edit: I get it now; the 2012 CCES re-interviewed some of the 2010 respondents and they could doublecheck the citizenship status variable).  I am also struck by John Ahlquist and Scott Gehlbach’s 2014 piece pointing out that the suprisingly high percentages of non-citizens reporting they are registered to vote may actually be referring to being registered to vote in their countries of origin.

Do 40% of police families experience domestic violence?

“As the National Center for Women and Policing noted in a heavily footnoted information sheet, ‘Two studies have found that at least 40 percent of police officer families experience domestic violence, in contrast to 10 percent of families in the general population.‘” — Conor Friedersdorf, The Atlantic, 9/28/14

The National Center for Women and Policing website is currently down, but we can use the Wayback Machine to see what Friedersdorf is citing.  The two studies cited by the Center are:

Johnson source

The Johnson source is the testimony of Leanor Boulin Johnson who at the time was a professor in the Department of Family Studies at Arizona State University (she currently is emeritus at ASU).  Johnson explains she surveyed 728 officers and 479 police spouses in “two East Coast police departments (moderate to large in size)”.  She says the sample was drawn in 1983, so presumably the survey was conducted in that year. There is no information on response rates nor how officers were selected, nor how they were invited to participate.  The 40% figure is mentioned on page 42:

Ten percent of the spouses reported being physically abused by their mates at least once; the same percentage claim that their children were physically  abused. The officers were asked a less direct question, that is, if they had ever gotten out of control and behaved violently against their spouse and children in the last six months.  We did not define the type of violence. Thus, violence could have been interpreted as verbal or physical threats or actual physical abuse.  Approximately, 40 percent said that in the last six months prior to the survey they had behaved violently towards their spouse or children.  Given that 20-30 percent of the spouses claimed that their mate frequently became verbally abusive towards them or their children, I suspect that a significant number of police officers defined violent as both verbal and physical abuse.

Neidig et al Source

Like the Johnson study, the Neidig et al. study relies on survey self-reports of police officers.  They surveyed 385 male officers, 40 female officers, and 115 female spouses who were apparently attending in-service training sessions and law enforcement conferences “in a southwestern state” (presumably Arizona; Neidig’s co-authors Harold Russell and Albert Seng’s institutional affiliation was listed as the Tuscon police department).

To measure domestic violence, they used the “Modified Conflict Tactics Scale” which gives subjects a list of 25 conflict behaviors and asks them to report the number of times they had engaged in each of them during the past year on a “7-point scale ranging from ‘never’ to ‘more than 20 times a year'”, although in their analyses they collapse this into “never” versus “ever”.   They give examples of items constituting “minor” and “severe” violence:

They present their findings in this table.

I am a little unsure how to interpret it, but they say that the “reported perpetrator, either self, spouse, or both, of the violence is listed” so I think this means that 28% of male officers report inflicting either “minor or severe” violence on their spouse and 33% report receiving minor or severe violence from their wives; 33% of wives say they inflicted minor or severe violence on their spouses, and 25% of police wives say they have received minor or severe violence.  What is noteworthy is that both male officers and wives’ reports agree that wives are a little more likely to commit any violence than are the officers.

The NCWP factsheet alluded to a comparison with the general population; this apparently also came from the Neidig et al. paper which used 1985 survey data from the National Family Violence Resurvey.  Neidig et al. do not talk about how the survey measured domestic violence but looking at the user’s guide (p. 56) suggests the two surveys used comparable items.  Neidig et al.’s tabulation comparing rates of domestic violence for law enforcement and civilian families uses the male police officer’s survey reports (not the survey reports of the police wives nor those of female officers).  As Neidig et al. say, it looks like rates of severe violence are pretty similar for law enforcement and civilian families; the main difference appeares to be in rates of “minor” violence.

Wrap Up

I confess that when I started this statistical scavenger hunt, I was expecting eventually to find this statistic was crap, but indeed there were two independent studies in the early 1990s showing that domestic violence is pretty common in police families.  However, the Johnson statistic is just referring to domestic violence committed by police officers; the Neidig et al. statistic is referring to domestic violence committed by either police officers or their spouses–if we just focus on police officers in the Neidig et al. study the figure is 28% which is still pretty high.

I am not crazy that the Neidig et al. study appears to be using a convenience sample and that both studies are pretty vague on recruitment.  On the other hand, I would expect that any sampling bias would run in the direction of underestimating domestic violence.  That is, officers who do perpetuate domestic violence would be less likely to volunteer to take a survey measuring various forms of personal and professional dysfunction.

 

 

 

 

Does the US have too stringent a lockdown policy?

On Wednesday, the economist Phil Magness posted this tweet with a graph from OurWorldInData (which I reproduce because his graph is hard to read in his tweet).

I have looked at different take-downs of the U.S. policy response to COVID, and a supposed late start of lock-downs has not been a prominent theme.  Mostly writers have been focusing on the lack of testing, the lack of protective gear for medical workers, Trump’s idiotic pronouncements about the virus, and Trump’s mismanagement of Sino-U.S. relations (e.g. Vox 6/8, Atlantic 6/28, Time 7/1, USA Today, er, yesterday).  But maybe Magness has a point.  Early on during the pandemic there was ire directed towards the federal government’s lack of guidance and devolving responsibility to states, municipalities, and private actors (see Atlantic 3/14).  And now people are making the connection between states’ re-opening and the new surge in COVID-19 cases (e.g. New York 6/29).

Or does he?  The graph he posted uses data from the Oxford COVID-19 Government Response Tracker (OxCGRT) put together by researchers at the Blavatnik School of Government at the University of Oxford.  The OxCGRT is an index (also known as a scale), that is, a statistic that aggregates (usually through summing or average) measures of different but related concepts to get the best measure of some broader concept.  One index that statistics professors have a lot of fun with are college rankings, as the inclusion and weighting of different measures/concepts tend to be pretty arbitrary, especially with the U.S. News and World Report rankings.  Joel Best, in More Damned Lies and Statistics, says that we risk turning such indices into magical numbers where we do not pay attention to the decisions that went into creating the index, and hence accord them an authoritativeness they do not deserve.

Magness’s graph focuses specifically on the OxCGRT’s “stringency” index (they have multiple indices).  This index is based on nine measures:

  • C1 • School closings (0-3)
  • C2 • Workplace closings (0-3)
  • C3 • Cancellation of public events (0-2)
  • C4 • Restrictions on private gatherings (0-4)
  • C5 • Closing public transport (0-2)
  • C6 • Stay at home requirements (0-3)
  • C7 • Restrictions on internal movement (0-2)
  • C8 • International travel controls (0-4)
  • H1 • Public information campaigns (0-2)

Having looked into the construction of this index, I would be cautious about using it make comparisons over time, but especially between countries (as Magness does).  There’s a couple of problems with the index:

First, there is the matter of actually quantifying government responses to COVID.  The OxCGRT team are not very clear on how exactly they took public information and scored it.  I am not sure what sources they consulted to score government actions (I am guessing news reports?).  Plus, deciding what value to assign a country seems to involve a level of personal discretion for the coder.  Take, for example, measure C2, workplace closings.  Their codebook describes the meaning of the four possible values this measure can take:

  1. no measure
  2. recommend closing (or work from home)
  3. require closing for some sectors or categories of workers
  4. require closing for all-but-essential workplaces (e.g. grocery stores, doctors)

The difference between 2 and 3 is quite blurry, especially depending on how broad a country defines “essential” workers. Bear in mind, the OxCGRT team–consisting of six primary investigators and over 120 contributors–are measuring these things for each country twice a week.  Maintaining consistent coding for many cases over so many dates, and coordinating this across over a hundred people seems terribly daunting to me.

But set this aside.  These are public policy scholars, maybe we can trust their subjective assessments.  But we have another issue–what do they do about intra-national heterogeneity in policy response?  After all, in the United States, state governments, not the national government, have been making the call to “lockdown” or “reopen”.  Here is what the OxCGRT team say:

Government coronavirus policies often vary by region within countries. We code the most stringent government policy that is in place in a country, as represented by the highest ordinal value. Sometimes the most stringent policy in a country will only apply to a small part of the population.

This is a big, big problem.  In other words, a country like the United States is being recorded as having the policy response of the most stringest state.  Magness wants to use this graph to compare the US to other European countries, and conclude that the U.S.’s policy was just like other European countries’, but the reality is that the U.S. has an unusual federal system of government with a lot of power delegated to the states.  By using the OxCGRT index, he is really comparing the stringest state to other European countries.  He is stacking the deck in favor of his conclusion that the U.S. was like other European countries and is not suffering from a lack of lockdown.

Now, all is not lost for Magness’s case.  The OxCGRT team have a statistical fix for this issue: if a country has a COVID policy response that was “targeted”, the country’s score for that particular indicator is penalized.  But here is where you can see all of the cumbersome, arbitrary decisions that go into index construction.   How is that score penalized?  By half a point.  So, in the United States, for most of the lockdown period it has been coded as “3” on the “workplace closings” indicator, meaning “require closing for all-but-essential workplaces”.  When the OxCGRT team aggregate the measures into the stringency index, they express them as out of 100, so the U.S.’s score without the penalty would be 3 out of 3, or 100%.  But the OxCGRT data record nearly all of the U.S. policies as “targeted”, so the score that the OxCGRT index actually uses when it creates the stringency index is not 3/3 but 2.5/3, or 83.3% (the half point penalty turns into a 17 percentage point penalty).

But if you look at my list above, you can see that not all of the measures have a range of 0-3.  Cancellation of public events has a range of 0-2.  For most of the lockdown period, the U.S. is coded as 2/2, but since this policy was targeted in the U.S., the score used to construct the index is 1.5/2, or 75% (the half-point penalty turns into a 25 percentage point penalty).  Likewise with restricting private gatherings: the U.S. is again mostly coded as 4/4, but again, this is targeted, so the score used to construct the index is 3.5/4 or 87.5% (the half point penalty turns into a 13 percentage point penalty).  So the fact that the U.S. has a federal system results in a penalty that is alternatively 13, 17, or 25 percentage points.  See how arbitrary this is?  And are these penalties even in the correct ballpark for evaluating how “targeted” or “general” a policy is in the United States?  Beats me, but it is also evident that is something the OxCGRT people are not concerned with.  But this index allows someone with an agenda, who wants to argue that the U.S. has had too much lockdown, to use this scale to push that argument without really thinking about how to compare a federal system like the U.S. to more centralized governments.

If you want to see how unique the U.S. is among the countries in the OurWorldInData graph, for each measure, here is the proportion of times the policy was coded as “general” (as opposed to “targeted” by OxCGRT.

Essentially, for all of the days and aspects when and where the United States was coded as having a COVID-19 containment policy,  only in 13 percent of them were they general policies.  The country that comes next after the United States in relying on targeted policies?  That is Germany, which is not surprising since the U.S. imposed the federal model on Germany after WWII.  What is surprising is that even a federal system like Germany still has general policies in 49 percent of the days and aspects.  The remaining countries are at 77 percent or higher.

If I were a libertarian and wanted to argue that lockdowns were not the solution to COVID-19, and that the U.S. has had too much lockdown, I would probably not take too much solace in the OxCGRT data.  If anything, I would be worried by the implication of the federal system in a government’s failure to respond to COVID-19.

 

Native American Attitudes Towards The Name of Some Football Team

Half a year ago, psychologist Stephanie Fryberg and her colleagues published an article (supplementary materials) in Social Psychological and Personality Science on how Native American identity influences attitudes towards sports’ teams use of native mascots, with a particular focus on the infamous Washington Redskins.  Jane Recker wrote a news article about the research for The Washingtonian.  In it, Recker compares Fryberg et al.’s findings to those of previous polls:

In 2016, the Washington Post published a poll about whether Native Americans found the Washington Redskins’ name offensive. Ninety percent of respondents said they were not offended by the team’s name. The poll has since been used by Dan Snyder and other team owners as evidence that their Native American mascots are inoffensive.

But a new study from academics at the University of Michigan and UC Berkeley contradicts that data. In a scientific survey of more than 1,000 Native Americans, roughly half of the participants said they were offended by the Redskins’ name.

 

Question wording and results from the Washington Post poll

 

Question wording and results from Fryberg et al. survey

In Recker’s interview with Fryberg, she speculates that the profound indifference shown by the Native American respondents in the Washington Post poll is due to question order effects and social desirability bias:

They called people, as part of a larger study, and they had these items [about mascots] in there. One of the things that we know in science is that the questions you ask before and after influence the response. For example, if I asked you a really serious question about people who are dying in your community, and then I say, “By the way, are you offended by Native mascots?” you see how you can really influence people. People have requested to know what the items were and what order they were in. The second issue is that they called people. There’s very good data that shows when you do a call versus online, it changes peoples’ responses. When you call, people are more likely to give positive and socially desirable answers. And then they only allowed as answers to their question, “are you offended, are you indifferent, are you not bothered?” Native people telling a person they don’t know that they’re “offended,” that’s a strong emotion…We took the same question [the Post asked], but we gave participants a one-to-seven scale. So you can answer, “I’m somewhat offended, I’m moderately offended, I’m extremely offended.” We also didn’t call them, we allowed them to do it online. There’s no stranger or other person you’re trying to account for, [worrying] what they’re going to think about your response.

Since Fryberg et al.’s poll differs from the Washington Post‘s poll in many different ways we have a “small-n big-p” problem–we have only two studies that differ in so many different ways it is impossible to tease out what exactly explains the difference between their findings.   Part of me wishes Fryberg and her team had retained the Washington Post‘s response set, or at least did a survey experiment and randomly assigned people to either the original response set or her response set, but the truth is replicating the Washington Post poll was only a secondary concern for these authors.

Alternative Explanations for the Difference Between the Post and Fryberg et al.

There are a couple of additional explanations for the differences between the two surveys. One is the Washington Post poll was fielded from December 2015 to April 2016, while Fryberg et al.’s survey was fielded more recently, and that maybe the cultural zeitgeist surrounding the Redskins has changed during the elapsed time.  I could not find in Fryberg et al.’s paper the exact days their survey was fielded, but I am guessing it was probably late 2018 to early 2019, so around three years after the Washington Post study.  Maybe over this time activists were able to mobilize greater antipathy to the “Redskins” name.  This is a possibility but it is a weak one–2019 was not that different from 2016.

A more plausible explanation is that the two surveys’ samples used quite different recruitment strategies and thus you are not quite getting comparable slices of Native American opinion for the two time periods.  Fryberg et al. sells their online survey as a strength–people are less susceptible to social desireability bias when doing a survey on the computer rather than the phone.  On the other hand, in my view this is a serious potential weakness, since recruiting people online risks getting self-selection bias in ways that recruiting people through phone calls does not. The Washington Post sample is substantially older and less educated than Fryberg et al.’s panel, which is about what one would expect.  The Washington Post sample is also educationally closer to the monoracial Native American population (according to the 2018 American Community Survey) than is Fryberg et al.’s survey, although the Washington Post sample is also better educated than the Native American population.  From the Washington Post‘s demographic table I posted below, one can see the Post used sample weights to counteract the selection biases their phone poll introduced.  As best as I can tell, Fryberg et al. did not use sampling weights.  It is likely that the younger, more educated, and more online Native American respondents in Fryberg et al.’s sample are more attuned to the outrage over the offensive “Redskins” name than are the less-educated, older Native American respondents in the Washington Post poll.  My strong suspicion is that if Fryberg et al. used a sampling strategy consistent with that of the Post the differences between the two findings would be much more muted (if they exist at all).

 

Demographics From Washington Post poll
Demographics from Fryberg et al.’s survey

 

My tabulations, from Census table B15002C

I would guess that this is not terribly relevant for Fryberg et al.’s central research question–the influence of Native American identity on attitudes towards team names.  It is much more consequntial for the univariate question of how much Native Americans find team names offensive, and in my view, it was a mistake for Fryberg to use that as a hook for media attention.

I also wonder if there are differences in how the two surveys categorized subjects as Native Americans.  It appears the Washington Post poll asked respondents to place themselves in one of seven racial categories: Asian, Black/African American, Native American, Pacific Islander, White, Mixed Race, and Other.  Only people who answered “Native American” were included in the study.  Fryberg et al. indicate they also used some kind of self-categorization into the “Native American” category as a criteria for inclusion in the study, but it was not clear to me if this includes individuals self-categorizing as just “Native American”  or as “Native American” plus some other group.  According to the 2018 5-Year American Community Survey, 2.7 million Americans self-categorized solely as “Native American”.  2.9 million Americans self-categorized as “Native American” plus one or more other group (people self-categorizing as “Native American” and “White” make up 1.9 million individuals alone).  Does Fryberg et al.’s study just focus on the  “monoracial” Native Americans, or do they also include the “multiracial” Native Americans?  I would guess that it is the former, since a sample including multiracial Native Americans would probably show even fewer Native Americans taking offense to the “Redskins” name, but I do not really know.

Too Many Notes

I want to make some other points about the Fryberg study.

One, the paper had a really sophisticated approach to measuring Native American identify.  While their sample just consists of people who categorize themselves as “Native American”, they measure different ways in which people identify as Native American: there’s legal status, there’s engagement with Native American cultures, and there is identity centrality.

Two, having said that, I probably would not have shown the simultaneous effects of these three measures of identity in the same model–I was really curious how people who are “legally” Native American react to the Redskins name, while Fryberg et al. show that, if anything, individuals who are legally Native American are less likely to agree the Redskins name is offensive, but they also control for the other measures of Native American identity.  Unless you are doing some kind of mediational model, there is not much point in comparing two Native American individuals, one legally defined as being Native American, the other not, but both have the same engagement with Native American culture and being Native American is equally central to their personal identities.

Fryberg’s regression table looking at the effects of identity on attitude towards the Redskins team name. Note that higher values mean greater agreement that the team name is offensive.

Three, the authors to their credit place a lot of information, including their survey, online, which is great for open science.

Four, if you look at the survey, you will see they asked their respondents a lot of questions.  In addition to 12 questions asking about feelings towards Native American mascots and team names and 67 questions about Native American identity (of which they used only 24 in the published study), they asked an additional 47 questions asking subjects’ opinions about various Native American issues that are not touched on in the article.  I really worry about the cognitive load these lengthy surveys put on respondents and I wonder about the quality of the data one gets.  Like many other researchers, Fryberg et al. attend to measures of reliability like Cronbach’s alpha, but I am not sure that a high reliability means a researcher does not have to worry about noisy measures.  A high Cronbach’s alpha just means that the items in the measure have a healthy correlation with each other.  But if respondents are tired, and they see a block of questions asking about similar things, they might just quickly decide on a general attitude and answer each question with that in mind without really thinking about the content of the questions (or really the point of the questions).  Thus, a block of questions could have a high reliability in the sense that people’s answers to them are correlated, but the overall scale may be an unreliable measure of the concept in the sense that if you asked the same person to take the scale on a different day they might settle for a very different general attitude that drives their answers to the items.  Having taken tedious surveys before this does not seem like a far-fetched scenario to me.

 

 

 

 

Quantifying police killings part 2

Last month the Police Policy Initiative disseminated a blog post putting police killings in the United States in international context:

 

 

To its credit, the PPI included a list of sources for its numbers.

One thing that caught my eye was that the number of police killings for the United States comes from the Mapping Police Violence project’s count for 2019, which is substantially smaller than that of the Fatal Encounters project.

Now, both projects rely on media reports to estimate their counts, and in fact Mapping Police Violence says they rely on Fatal Encounters (as well the U.S. Police Shootings Database and KilledbyPolice.net).  The difference between FatalEncounters and Mapping Police Violence is that Mapping Police Violence excludes suicides and car crashes.  When I wrote the first blog post on this I forgot that FatalEncounters did include such incidents:

We try to document all deaths that happen when police are present or that are caused by police: on-duty, off-duty, criminal, line-of-duty, local, federal, intentional, accidental–all of them. 

This is a very broad conceptual definition; Mapping Police Violence’s is a bit narrower:

Police Killing: A case where a person dies as a result of being shot, beaten, restrained, intentionally hit by a police vehicle, pepper sprayed, tasered, or otherwise harmed by police officers, whether on-duty or off-duty.

Again, this reiterates Joel Best’s point about the importance of conceptual breadth for understanding discrepancies in statistics.  Arguably, my mistake also illustrates Joel Best’s point about mutant statistics, where people, intentionally or otherwise, garble the meaning of statistics.  In my previous post I used the term “police killings” to describe the incidents counted by FatalEncounters, which was a mistake, as FatalEncounter clearly includes incidents where the deceased died by suicide or in a car crash (while being followed by the police).

But the international comparisons are the main point of this post.  They are really striking, and other outlets (Axios, The Economist, Vox) have also noted the large discrepancy between the US and other countries in terms of police killings.

Of the countries listed in the PPI graph, I wanted to see the source of the figure for Japan, as that is the largest country of those mentioned in the graph.  PPI lists the aforementioned Axios article as the source of the Japan data, and Axios doesn’t give a source.  Googling “police killings in Japan” (without the quotes) turns up a Wikipedia article which I suspect is the source for Axios.   Like the Axios piece, Wikipedia lists a count of 2 police killings in 2018, and its source is two media reports, one about a police shooting in Sendai and another about a police trainee in Hikone killing his supervising officer for being too mean (which is probably not the kind of incident an American, trying to conjure up the ideal-typical police killing in her mind, would come up with).  It seems a bit lame to me that news outlets and think tanks are passing along Wikipedia facts without confirmation.  The most recent count when the Economist article appeared in 2014 was a big fat 0; the Economist article is paywalled and the text of the article that I accessed via ProQuest does not mention Japan (my assumption is the Economist article, which was cited by Vox for the zero-police-killings-in-Japan-figure, had a graph showing this number that does not appear in the databases) but I do not know where this came from.  If people are really tallying up the number of police killings in Japan by relying on English-language news reports of such incidents I would be very skeptical of that figure; but given Japan’s extremely strict gun control I would not be surprised if it is close to the truth.

If we turn to other major Anglophone countries, Canada’s count comes from journalists who are not very clear on their methodology, but they appear to be applying FatalEncounters’s broad conceptual definition: “every person who died or was killed during a police intervention”.  The journalists mention that Canada does not have official statistics on fatal police encounters so I am guessing that, like FatalEncounters, they had to rely on news accounts.  The figure for England-Wales comes from a charity dedicated to “state related deaths” (explicitly saying that their mission is only for those two countries in the United Kingdom).  Their definition is much narrower: they count up the number of “people who have died as a result of police shootings” so their definition is more inline with the Washington Post’s database that I mentioned in my earlier blog post.

As Joel Best talks about in Damned Lies and Statistics, we really have to be careful about making international comparisons.  In this case, PPI took figures for different countries that were constructed by different actors using different definitions.  Fortunately for PPI, the inconsistent definitions are not fatal for the point they are making: police killings, while still very rare in the U.S., are much, much rarer in other countries.