Category Archives: Research

Data-driven Discovery of Governing Equations of Li-ion Batteries Pertaining State of Charge

Research

The complex electrochemical behavior of batteries results in nonlinear and high-dimensional dynamics. Accurate SOC prediction is paramount for increased performance, improved operational safety, and extended longevity of LiBs. The battery’s internal parameters are cell-dependent and change with operating conditions and battery health variations. We present a data-driven solution to discover governing equations pertaining to SOC dynamics from battery operando measurements. 

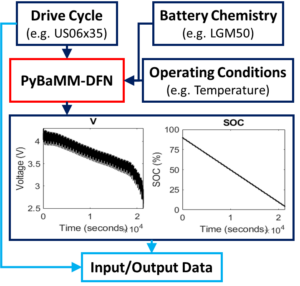
Schematic of Data Collection Process

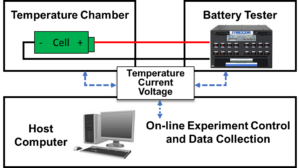
Schematic of Experimental Setup

Our approach relaxes the need for detailed knowledge of the battery’s composition while maintaining prediction fidelity. The predictor consists of a library of candidate terms and a set of coefficients found via a sparsity-promoting algorithm. The library was enhanced with explicit physics-inspired terms to improve the predictor’s interpretability and generalizability. Further, we developed a Monte Carlo search of additional nonlinear terms to efficiently explore the high-dimensional search space and improve the characterization of highly nonlinear behaviors. Also, we developed a hyperparameter autotuning approach for identifying optimal coefficients that balance accuracy and complexity.

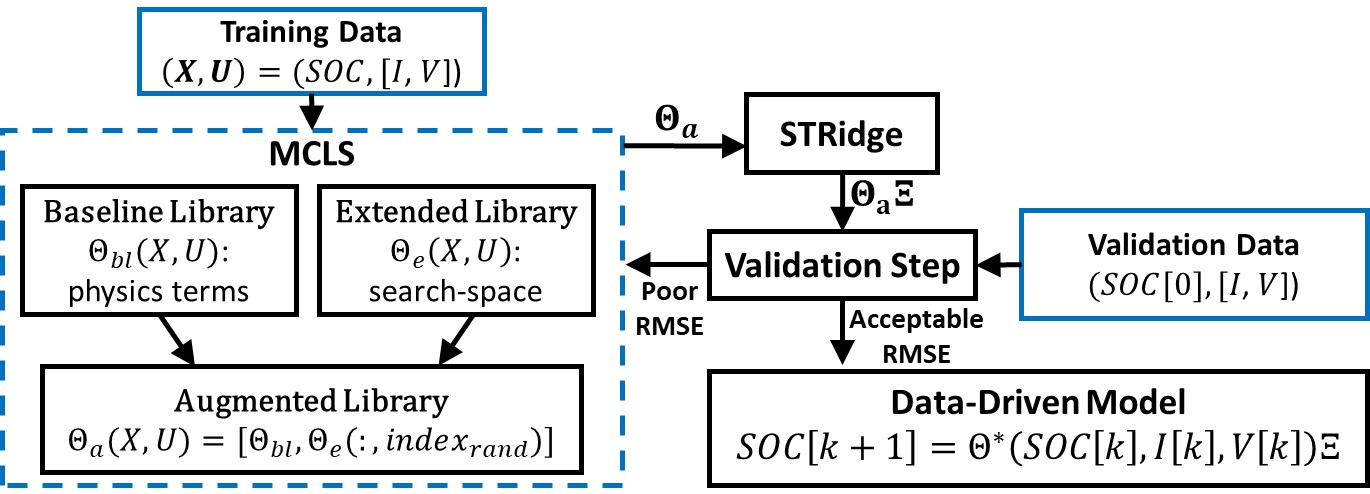
Schematic of Monte Carlo Library Search (MCLS)

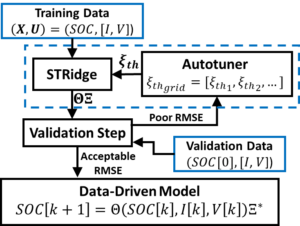
Schematic of Hyperparameter Autotuner

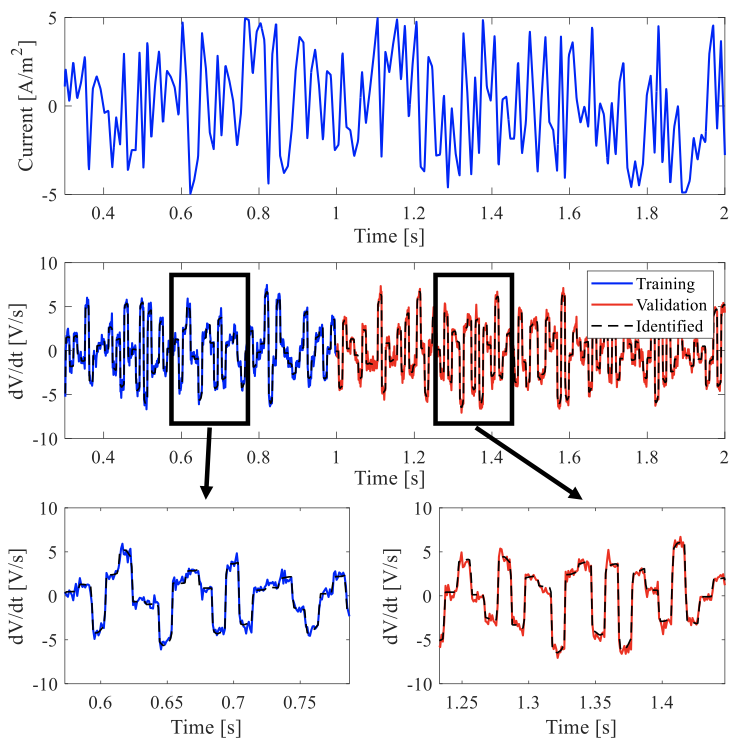
We tuned the model’s performance and sparsity by exploring different combinations of candidate terms (basis functions) and data sampling rates. The resulting SOC predictor achieved high predictive performance scores (RMSE) of 2.2e-6 and 4.8e-4, respectively, for training and validation on experimental results corresponding to a stochastic drive cycle.

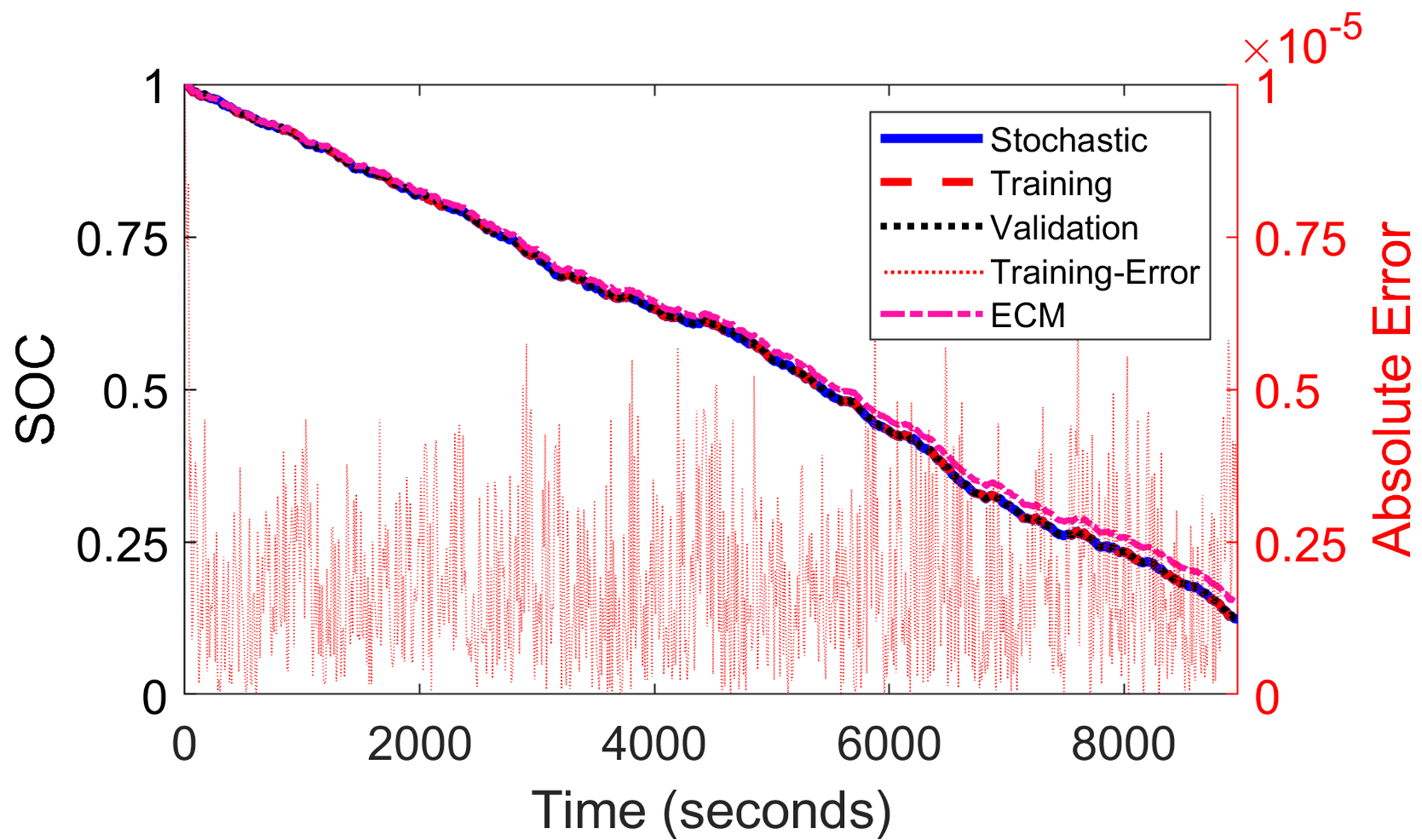
Training Results and Model-Validation to predict SOC from current, voltage, and initial SOC (Experimental Data)

The predictor achieved a generalizability RMSE of 8.5e-4 on unseen battery measurements corresponding to the standard US06 drive cycle, further showcasing the adaptability of the predictor and the enhanced modeling approach to new conditions.

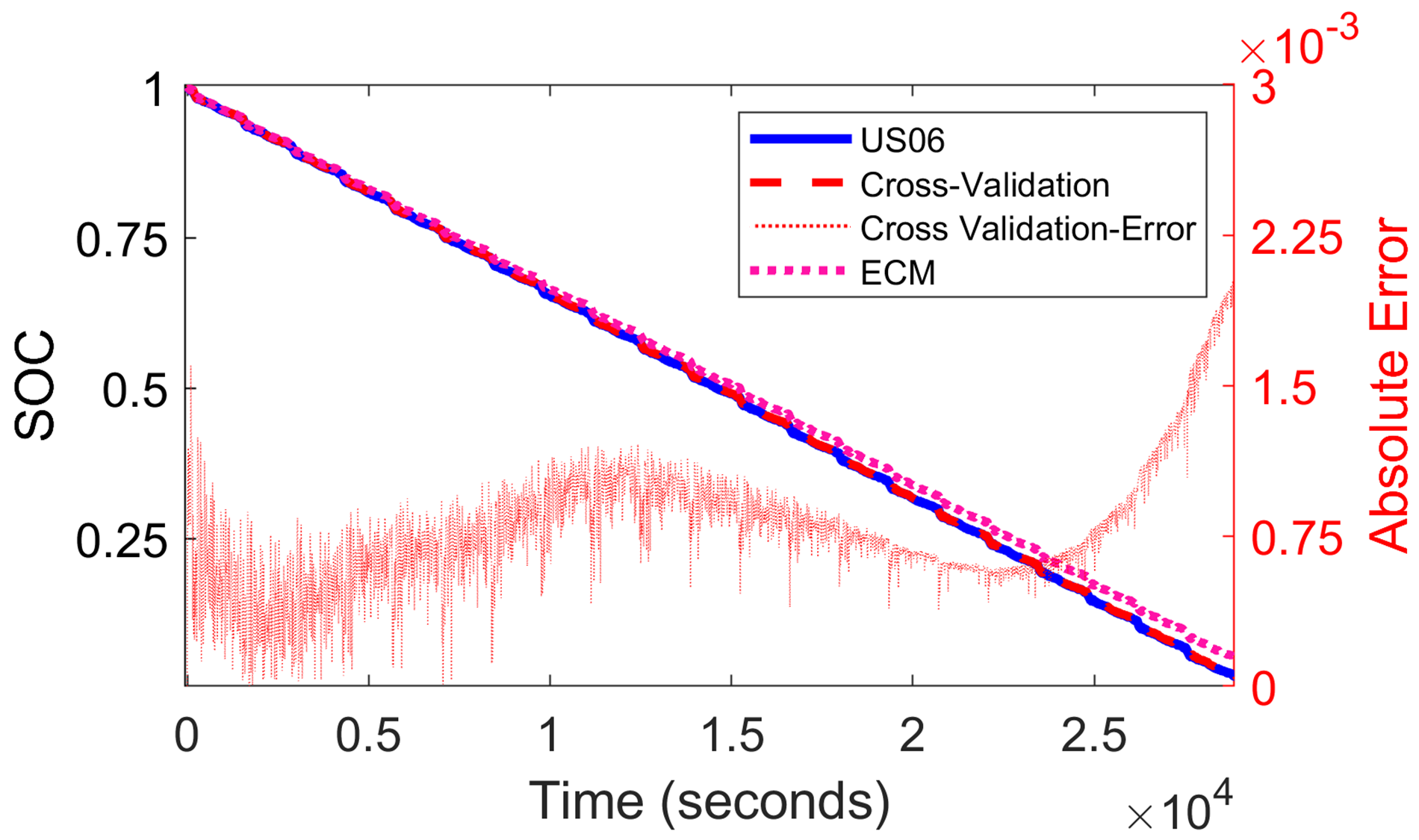
Cross-Validation (Generalizability) Results on unseen battery measurements

The modeling technique includes explicit physics-inspired terms, which allows for interpretable and generalizable models. Furthermore, the procedures and methods developed in this research are generic and can guide machine learning modeling of other dynamical systems.

Publications

Data-Drive Modeling of Complex Dynamical Systems

Research

Complex dynamical systems such as energy storage systems (ESS) have high-order models, which are costly to develop as they require the tedious task of determining the material and physical parameters of the system. We aim to mitigate these shortcomings by developing data-driven models of such systems from the input/output response data. We utilize tools from subspace identification, sparsity promoting regularization, and switching systems theory to determine the optimal time-varying data-driven models. Further, we develop Koopman operators’ modeling techniques and extend them to control ESS.

Identifying Li-ion battery model from measurable input-output data
Sparse-Data-Driven-Modeling-of-LiBsDownload

Publications:

Ahmadzadeh, O., Rodriguez, R., and Soudbakhsh, D. “Modelling of Li-ion Batteries for Real-Time Analysis: A Data-Driven Approach”, American Control Conference, 2022.

Optimal Control of an AC75 Sailboat for the America’s Cup Race

Research

This research presents an adaptive control scheme to achieve optimal sailing maneuvers for an AC75 foiling sailboat competing in America’s Cup, the world’s premier sailboat race. The innovative sailboat design introduces extra degrees of freedom and articulations in the boat that result in nonlinear, high-dimensional, and unstable switching dynamics. These complex dynamical characteristics make the optimization of this MIMO (multiple-input multiple-output) system via traditional methods prohibitive. Therefore, we presented an adaptive learning scheme to learn the Jacobian of the system from measurement data, and adapt the commands at each time step to achieve the optimal maneuvers.

Publications

Safety Evaluation of Li-ion Batteries

Research

Energy storage systems (ESS) such as Li-ion Batteries (LIBs) are the solution for many applications including cellphones and electric vehicles. However, they can pose serious hazards if their safety is compromised such as after sustaining mechanical damage. Lithium-ion batteries have several internal processes that contribute to their response to current excitation. There is a frequency range associated with each of these internal processes in which they are most active. Therefore, conducting EIS (Electrochemical Impedance Spectroscopy) experiments can be used to investigate the effect of different excitation/environmental conditions on these time constants. EIS is an important tool in analyzing and modeling ESS which is based on applying sinusoidal inputs in the form of voltage or current to the cell and measuring the output current or voltage. EIS plots provide the response of the system to a wide range of frequencies. However, due to the presence of several processes inside ESS, the interpretation of EIS data is a challenging task. Therefore, supplementary tools are needed to extract the required information from EIS data. Distributed Equivalent Circuit Model (DECM) and Distribution of Relaxation Time (DRT) are two main tools for analyzing EIS data. However, in the DECM approach, the number and type of circuit’s elements and their connection to the cell’s physics is still an open question. DRT approach can decouple the processes by identifying the time constants of the EIS data. However, the DRT method and its variations do not work on ESS due to their complex impedance spectra, which violates the underlying assumptions commonly used in DRT.

 

Schematic of Li-ion Battery components with different Electrochemical and degradation mechanisms vs Frequency.

In this research, we address characterizing the safety status of Li-ion batteries based on their time constants. We introduce a method to determine time constants of energy storage systems (ESS) using their impedance spectra. The Distribution of Relaxation Times (DRT) function has been suggested to determine such time constants. We formulated DRT as a ridge regression optimization. We introduced criteria (discrepancy, cross-discrepancy, and the normalized root mean squared errors) to determine the time constants as the peaks of the resulting distributed function. The proposed approach was validated using experiments on Li-ion batteries (LIBs). We measured the impedance spectra of LIBs using an EIS instrument at different cell temperatures ( to and State-of-charge ( and SOC). We determined the time constants and used the SOC and temperature data to assign the peaks to appropriate electrochemical processes and verified them using the experimentally calculated time constants reported in the literature. We hypothesize that the time constants of ESS can be used for their fault detection and health monitoring, such as after sustaining mechanical load/impact. To validate this hypothesis, we measured impedance spectra and determined time constants of intact and mechanically damaged 18650 cylindrical cells. The DRT peaks showed the main differences between these groups and suggested criteria to determine the extent of mechanical damage from the impedance spectra. The method has application in the fields beyond ESS, where the frequency response can be measured. The time constants determined using our proposed method can guide the control-oriented data-driven models as well as the equivalent circuit models of ESS. For example, the number of time constants can determine the minimum number of elements to model ESS as well as the range of frequency at which these elements are excited. Furthermore, the time constants (and the basis function) can be used for distributed modeling of ESS with many elements and used for their fault detection and health monitoring.

Publications:

  • Derakhshan, M., Sahraei, E., and Soudbakhsh, D. “Detecting Mechanical Indentation From the Time Constants of Li-ion Batteries, ” in Cell Reports Physical Science, 2022, doi: 10.1016/j.xcrp.2022.101102.
  • Derakhshan, M., and Soudbakhsh, D. “Temperature-Dependent Time Constants of Li-ion Batteries,” in IEEE Control Systems Letters, vol. 6, pp. 2012-2017, 2022, doi: 10.1109/LCSYS.2021.3138036.
  • Keshavarzi, M., Derakhshan, D., Gilaki, M., L’Eplattenier, P., Caldichoury, I., Soudbakhsh, D., and Sahraei, E., “Coupled Electrochemical-Mechanical Modeling of Lithium-Ion Batteries Using Distributed Randle Circuit Model,” 2021 International Conference on Electrical, Computer and Energy Technologies (ICECET), 2021, pp. 1-6, doi: 10.1109/ICECET52533.2021.9698796.
  • Derakhshan, M., Gilaki, M., Stacy, A., Sahraei, E., and Soudbakhsh, D. (January 22, 2021). “Bending Detection of Li-Ion Pouch Cells Using Impedance Spectra.” ASME. Letters Dyn. Sys. Control. July 2021; 1(3): 031005. doi: 10.1115/1.4049527.
  • Soudbakhsh, D., Gilaki, M., Lynch, W., Zhang, P., Choi, T., Sahraei, E. Electrical Response of Mechanically Damaged Lithium-Ion Batteries. Energies 2020, 13, 4284. doi: 10.3390/en13174284
  • Stacy, A., Gilaki, M., Sahraei, E., and Soudbakhsh, D. ”Investigating the Effects of Mechanical Damage on Electrical Response of Li-Ion Pouch Cells,” 2020 American Control Conference (ACC), 2020, pp. 242-247, doi: 10.23919/ACC45564.2020.9147883.
  • Sahraei, E., Gilaki, M., Lynch, W., Kirtley, J., and Soudbakhsh, D. “Cycling Results of Mechanically Damaged Li-Ion Batteries,” 2019 IEEE Electric Ship Technologies Symposium (ESTS), 2019, pp. 226-230, doi: 10.1109/ESTS.2019.8847923.

Cooperative path planning for multiple non-holonomic vehicles

Research

We present a metric space approach for high-dimensional sample-based trajectory planning. Sample-based methods such as RRT and its variants have been widely used in robotic applications and beyond, but the convergence of such methods is known only for the specific cases of holonomic systems and sub-Riemannian non-holonomic systems. Here, we present a more general theory using a metric-based approach and prove the algorithm’s convergence for Euclidean and non-Euclidean spaces. The extended convergence theory is valid for joint planning of multiple heterogeneous holonomic or non-holonomic agents in a crowded environment in the presence of obstacles. We demonstrate the method both using abstract metric spaces (l_p geometries and fractal Sierpinski gasket) and using a multi-vehicle Reeds-Shepp vehicle system. For multi-vehicle systems, the degree of simultaneous motion can be adjusted by varying t.he metric on the joint state space, and we demonstrate the effects of this choice on the resulting choreographies.

Trajectory planning for two car-like robots in a 100×100
cm2 region with obstacles using (a) L1-norm, (c) L2-norm, and
(e) L∞-norm. We show the starting pose of each vehicle using
dashed lines and arrows, and the final pose using solid lines
and arrows. Static environmental obstacles are shown as gray
boxes. The speed of each vehicle over time is shown in the
corresponding figures (b), (d), (f).

Publications

A. Lukyanenko and D. Soudbakhsh, “Sampling-based multi-agent choreography planning: a metric space approach,” Robotics and Autonomous Systems, In Press 2023.

Lukyanenko, A., and Soudbakhsh, D. “Sampling-Based Multi-Agent Choreography Planning: A Metric Space Approach,” 2021, arXiv: 2108.03191 [cs.RO]. (download the arxiv version) https://arxiv.org/abs/2108.03191

Lukyanenko, A., Camphire, H., Austin, A., Schmidgall, S., and Soudbakhsh, D.”Optimal Localized Trajectory Planning of Multiple Non-holonomic Vehicles,” 2021 IEEE Conference on Control Technology and Applications (CCTA), 2021, pp. 820-825, doi: 10.1109/CCTA48906.2021.9658995.