We present a metric space approach for high-dimensional sample-based trajectory planning. Sample-based methods such as RRT and its variants have been widely used in robotic applications and beyond, but the convergence of such methods is known only for the specific cases of holonomic systems and sub-Riemannian non-holonomic systems. Here, we present a more general theory using a metric-based approach and prove the algorithm’s convergence for Euclidean and non-Euclidean spaces. The extended convergence theory is valid for joint planning of multiple heterogeneous holonomic or non-holonomic agents in a crowded environment in the presence of obstacles. We demonstrate the method both using abstract metric spaces (l_p geometries and fractal Sierpinski gasket) and using a multi-vehicle Reeds-Shepp vehicle system. For multi-vehicle systems, the degree of simultaneous motion can be adjusted by varying t.he metric on the joint state space, and we demonstrate the effects of this choice on the resulting choreographies.
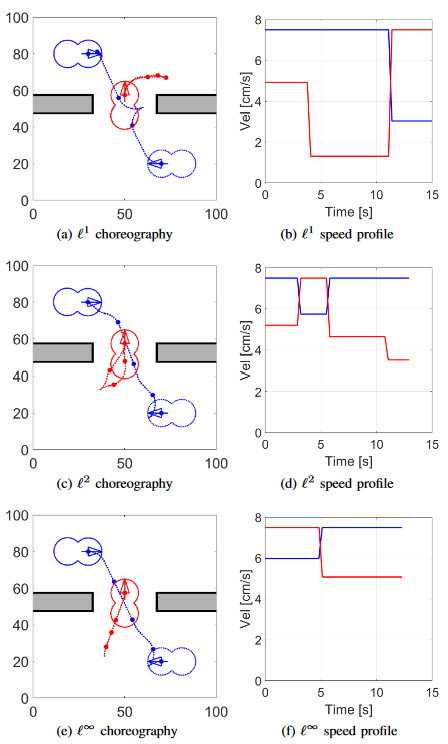
cm2 region with obstacles using (a) L1-norm, (c) L2-norm, and
(e) L∞-norm. We show the starting pose of each vehicle using
dashed lines and arrows, and the final pose using solid lines
and arrows. Static environmental obstacles are shown as gray
boxes. The speed of each vehicle over time is shown in the
corresponding figures (b), (d), (f).
Publications
A. Lukyanenko and D. Soudbakhsh, “Sampling-based multi-agent choreography planning: a metric space approach,” Robotics and Autonomous Systems, In Press 2023.
Lukyanenko, A., and Soudbakhsh, D. “Sampling-Based Multi-Agent Choreography Planning: A Metric Space Approach,” 2021, arXiv: 2108.03191 [cs.RO]. (download the arxiv version) https://arxiv.org/abs/2108.03191
Lukyanenko, A., Camphire, H., Austin, A., Schmidgall, S., and Soudbakhsh, D.”Optimal Localized Trajectory Planning of Multiple Non-holonomic Vehicles,” 2021 IEEE Conference on Control Technology and Applications (CCTA), 2021, pp. 820-825, doi: 10.1109/CCTA48906.2021.9658995.