Excited to share work now out in Journal of Chemical Information and Modeling :
Novack, Dylan, Robert M. Raddi, Si Zhang, Matthew F. D. Hurley, and Vincent A. Voelz.Simple Method to Optimize the Spacing and Number of Alchemical Intermediates in Expanded Ensemble Free Energy Calculations. Journal of Chemical Information and Modeling 65, no. 12 (2025): 6089–6101. https://doi.org/10.1021/acs.jcim.5c00704
First, we estimate the thermodynamic length between intermediates using a short expanded-ensemble (EE) simulation, and then use a cubic spline fit to do gradient-based optimization of the spacing.
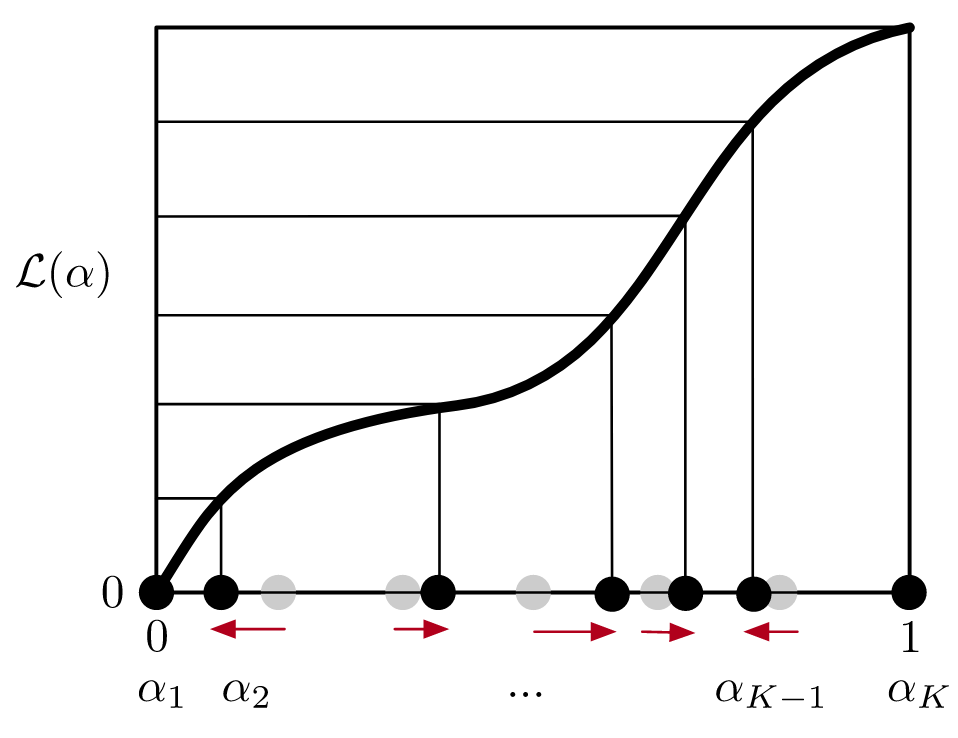
Using the same approach, we also optimize the number of intermediates used in EE simulations, which sample all intermediates during a simulation by proposing/accepting transitions between ensembles using Monte Carlo. Modeling this Markov process reveals the optimal number of intermediates that minimize the mixing time.
Here’s a result for a toy system of 1D harmonic potentials:
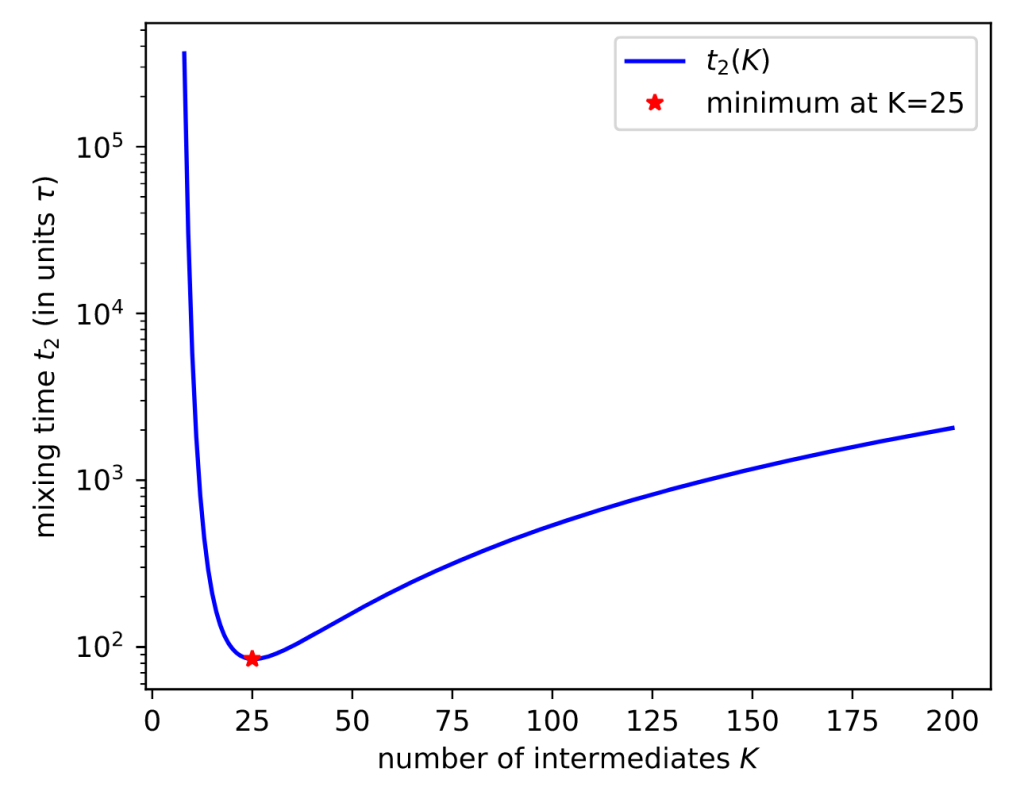
More mixing leads to smaller uncertainties. Sure enough, EE sampling with the optimal number of intermediates (K*=25) gives the lowest uncertainty.
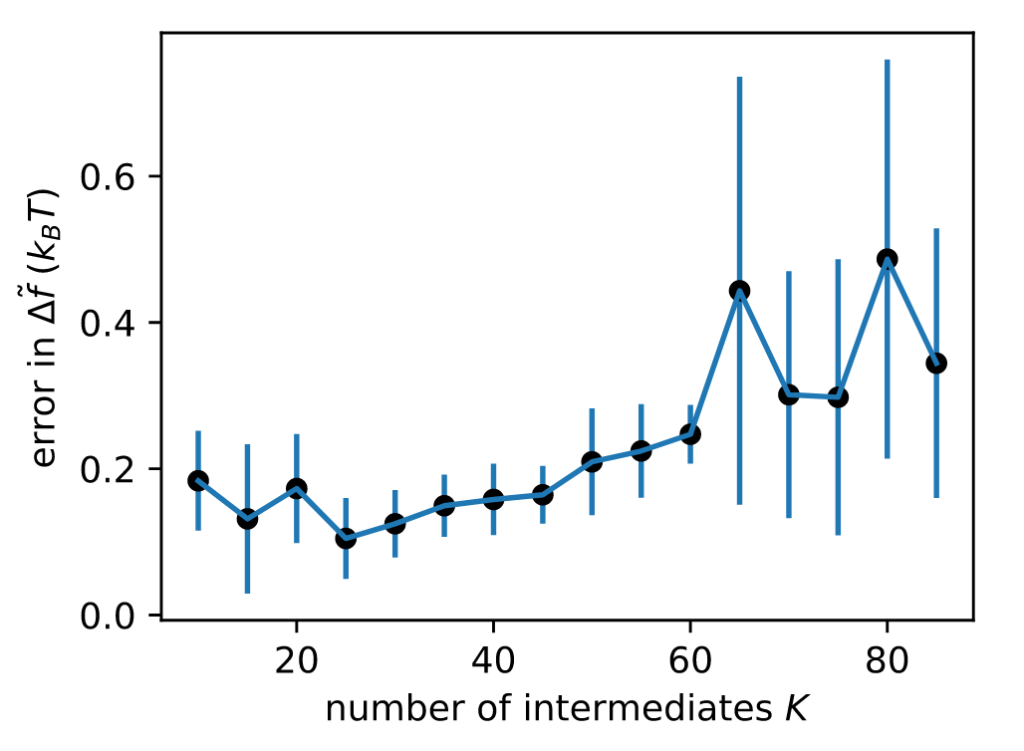
Does it work in realistic systems? You bet! Here’s a relative binding free energy calculation where we alchemically transform Ala to Phe using pmx in GROMACS. Optimized intermediates yield EE simulations that converge faster to accurate estimates.

Want to try it yourself? Check out our freely available Python scripts at https://github.com/vvoelz/pylambdaopt.
We also note that this approach should also work well for other methods using exchanges between thermodynamic ensembles (REMD or HREX), with some adjustments. It could also improve uncertainties in NEW. If you are interested, let us know!
–Vincent Voelz

