Journal Publications
• Dimitri Karagiannis, Verica Radisavljevic-Gajic. A Backstepping Boundary Observer for a Simply Supported Beam. IEEE Transactions on Automatic Control. 64(9): 3809 – 3816, 2019. doi: 10.1109/TAC.2018.2884677
ABSTRACT: This paper presents the development of a full-state observer for an Euler-Bernoulli beam system with simply supported boundary conditions. This problem is motivated by the necessity of estimators in control and diagnostic applications. The observer is developed using a backstepping procedure. The full state observer cannot be completed with a single observer system, and hence this paper presents the synthesis of two observer structures that together provide the desired convergence. The necessary feedback information is limited to the slope and the shear force of the beam at one boundary, which are practically measurable values on a physical system. The observer estimates the full infinite dimensional beam system without any discretization of the model. The result of the technique developed in this paper is that the infinite dimensional observer estimates converge to the plant system states (representing the actual beam displacement) at an arbitrary exponential rate; numerical simulation results validating this behavior are provided.
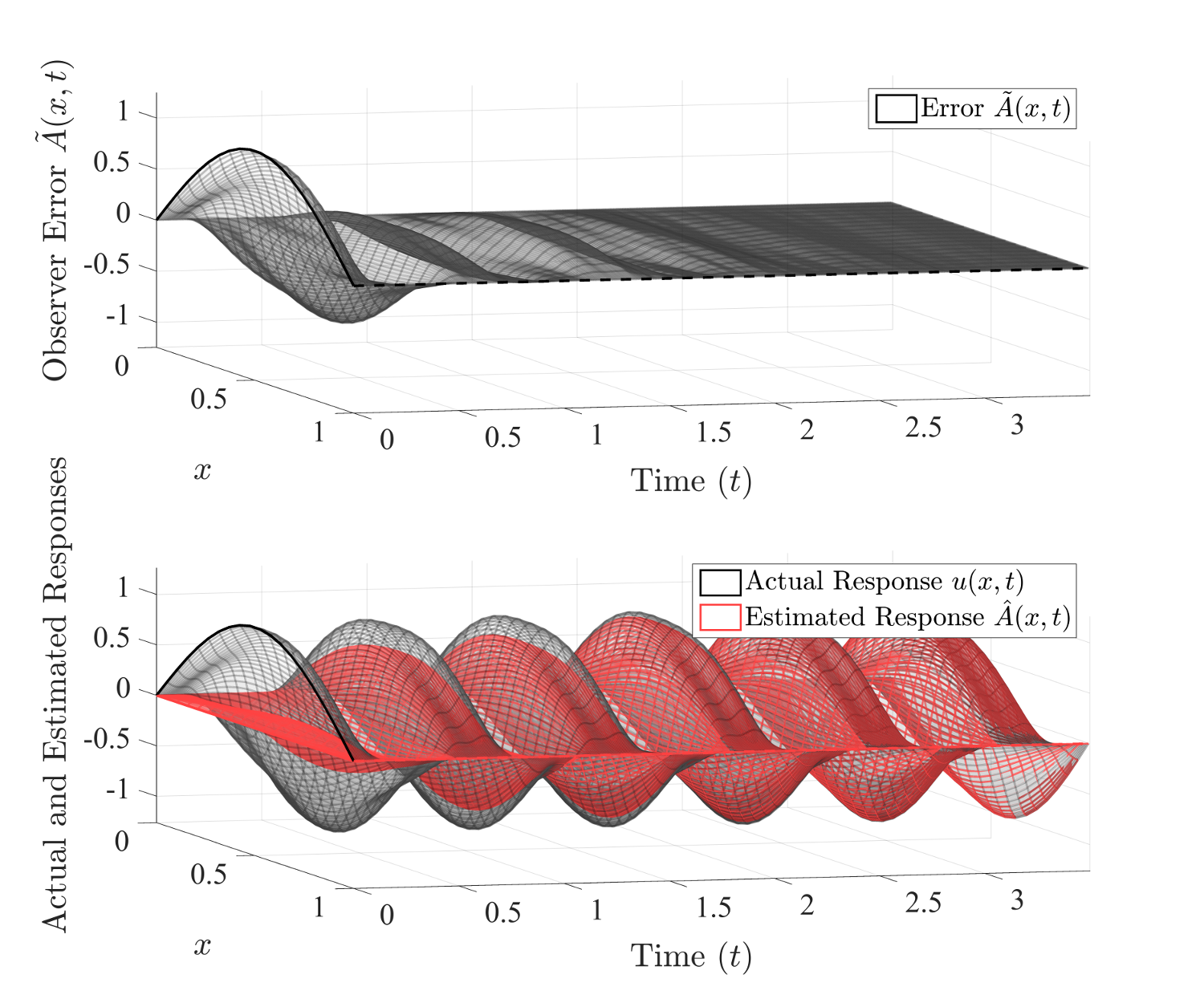
Observer error with respect to time along the length of an oscillating beam
• Dimitri Karagiannis, Verica Radisavljevic-Gajic. Exponential Stability for a Class of Boundary Conditions on a Euler-Bernoulli Beam Subject to Disturbances via Boundary Control. Journal of Sound and Vibration. 46: 387 – 411, 2019. doi: 10.1016/j.jsv.2019.01.020
ABSTRACT: This paper outlines the procedure for applying a sliding mode backstepping boundary control technique to a Euler-Bernoulli beam subject to unknown bounded disturbances on the boundary for four different types of boundary conditions, referred to in this paper as a ‘class’ of boundary conditions. These boundary conditions include all combinations of ‘pinned’ and ‘sliding’ types with control and disturbances on one boundary, i.e. pinned-pinned, pinned-sliding, sliding-pinned, and sliding-sliding with input on the second boundary. The technique was developed for the specific case of a pinned-pinned beam in the literature, and in this paper the technique is generalized to the degree that it is possible to cover all four of the aforementioned cases. Furthermore, a proof of the fully arbitrary, exponential stability of the closed-loop system is provided in this paper; to this point only asymptotic stability was shown for the closed-loop system for one case. The technique outlined in this paper provides, for a class of boundary conditions, a controller that exponentially stabilizes the vibrations in a beam in the presence of bounded unknown disturbances. The beam displacement returns to the origin and its decay is bounded by a known exponential decay function after a known finite-time reaching phase.
Exponential decay of the controlled states of a sliding-sliding beam
• Dimitri Karagiannis, Verica Radisavljevic-Gajic. Sliding Mode Boundary Control of an Euler Bernoulli Beam Subject to Disturbances. IEEE Transactions on Automatic Control, 63(10):3442 – 3448, 2018. doi: 10.1109/TAC.2018.2793940
ABSTRACT: In this paper a control technique is presented for an undamped, pinned-pinned Euler-Bernoulli beam with control inputs and bounded disturbances on one boundary. The control strategy developed drives the system to its origin at an arbitrary exponential rate in the presence of the disturbances. This is achieved in two main steps. First, a backstepping transformation is used to convert the marginally stable Euler-Bernoulli beam system to a new form that has an exponentially stable homogeneous form. Control inputs are needed to fully convert the system to this form, however since they are distorted by unknown bounded disturbances, the next step implements a sliding mode controller to account for them. The proposed sliding manifolds require a combination of classical and `second order’ techniques in order to avoid discontinuous chattering on the physical system. Therefore, the continuous sliding mode controllers developed return the beam to its origin at an arbitrary exponential rate, and do so in the presence of unknown bounded disturbances on the boundary. The main contributions of this paper with respect to previous backstepping designs for the Euler-Bernoulli beam are that all three of the following goals are accomplished together: (i) steady state position is the origin, (ii) decay rate has no theoretical restrictions, and (iii) is robust to bounded disturbances.
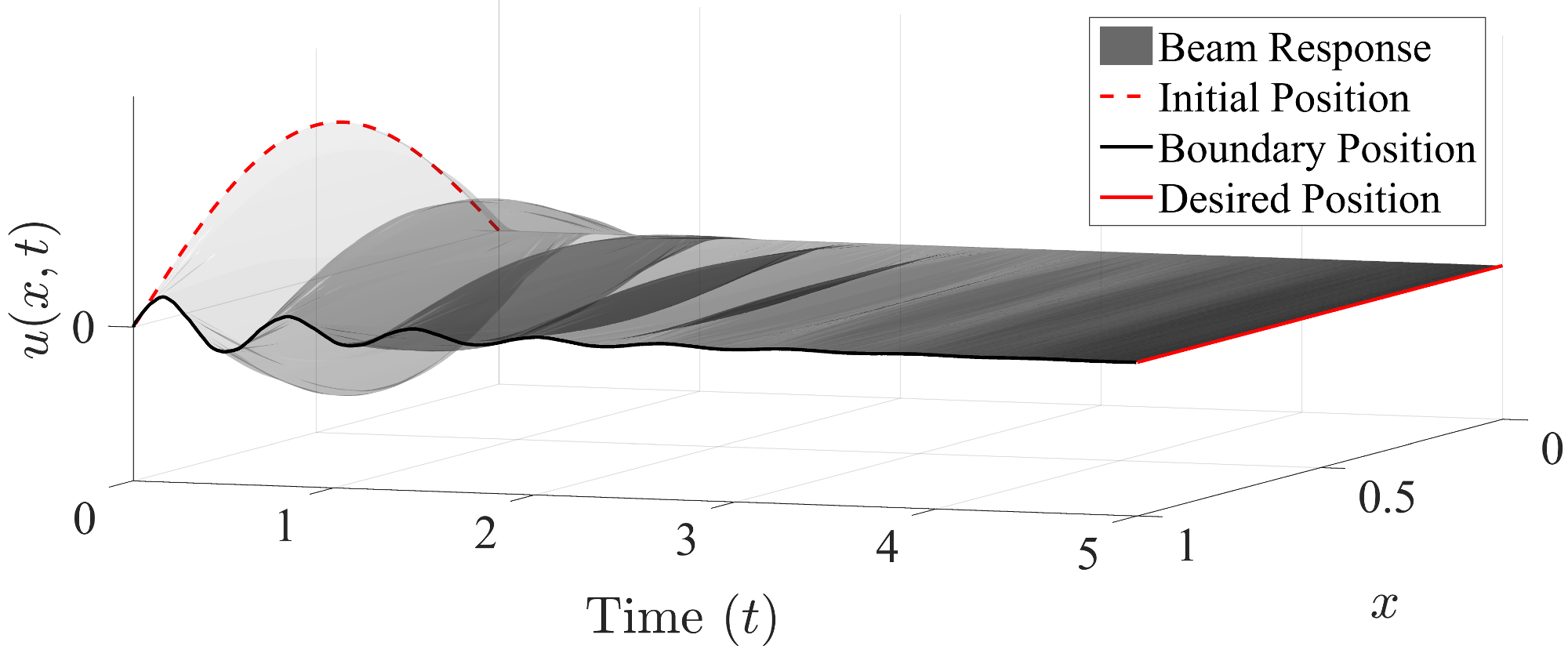
Controlled, exponentially stable response of a beam subject to unknown boundary disturbances
• Dimitri Karagiannis, Verica Radisavljevic-Gajic. Sliding Mode Boundary Control for Vibration Suppression in a Pinned-Pinned Euler-Bernoulli Beam with Disturbances. Journal of Vibration and Control, 24(6):1109-1122, 2018. doi: 10.1177/1077546316658578.
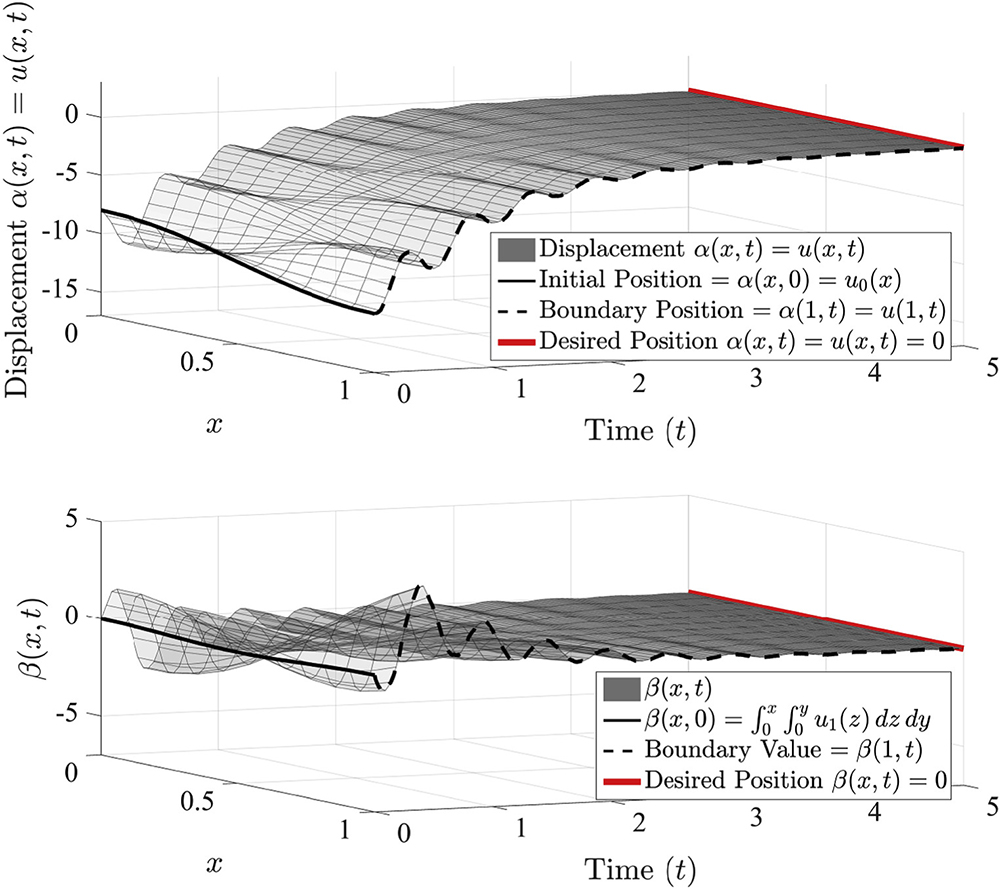
ABSTRACT: This work addresses the control of a pinned-pinned beam represented by the fourth order partial differential equation commonly known as the Euler–Bernoulli beam model. The system under consideration has pinned boundary conditions on one end (displacement and bending moment fixed at zero) and controlled boundary conditions on the other end (displacement and bending moment are prescribed by control functions). There are also unknown bounded disturbances included on the controlled boundary. A backstepping control technique which introduces arbitrary damping into the system is discussed, and a method for applying this control in the presence of unknown disturbances is developed using sliding mode control theory. Sliding mode controllers are developed in a way that does not create a chattering effect, which is a common issue with sliding mode control. Simulation results are presented to show how the system dampens out vibrations at an arbitrarily determined rate and how the control functions respond to unmodeled disturbances.
Simulation of a controlled pinned-pinned beam subject to disturbances; the system dissipates vibrations and settles to steady state position
• Dimitrios A Karagiannis, Garrett M Clayton, and C Nataraj. Boundary control of harmonic disturbances on flexible cantilever beams using piezoelectric patch actuators. Journal of Vibration and Control, 22(18):3916-3929, 2016. doi: 10.1177/1077546314567723.
ABSTRACT: This work addresses the control of vibrations in flexible structures caused by external harmonic disturbances using a boundary control method. The research is motivated by practical systems where beam-like structures require vibration suppression to prevent fatigue and system damage, or to increase efficiency. Importantly, this paper addresses a practical constraint of the actuation points being at the boundaries only. The method presented here is an open-loop control scheme which requires knowledge of the harmonic disturbance and a model of the flexible system. The controller uses the model, developed using the Rayleigh–Ritz method, to predict the reaction of the beam to the known input disturbance and compute an optimized control input which reduces the steady state vibration in the system. By properly choosing the cost function, the controller can be used to reduce the total vibration or to reduce the vibration in certain spatial locations. The method’s vibration reduction capabilities are studied over a range of frequencies; data collected from experiments on a physical beam model is used to validate the predicted behavior of the system.
Experimental test showing effectiveness of boundary controller to persistent harmonic excitation
Conference Publications
• Dimitri Karagiannis and Verica Radisavljevic-Gajic. On Boundary Observation of a Simply Supported Beam via a Backstepping Design. In American Control Conference (ACC), pages 3678-3682, Milwaukee, Wisconsin, USA, June 27-29, 2018. doi: 10.23919/ACC.2018.8431200.
ABSTRACT: In this paper the first part of a full-state boundary observer for a simply supported Euler-Bernoulli beam is developed using a backstepping method. The fourth order partial differential equation (PDE) system is first transformed into a second order coupled system using a variable transformation that has been developed and is to be published elsewhere. The feedback information available to the observer is limited to only two scalar values related to the slope and the shear force of the beam at one boundary. Using the methods developed in this paper, an observer is derived such that the estimate of the full beam displacement converges exponentially to the actual beam displacement. This is a necessary complement to the feedback control problem, where full state knowledge is required but is practically impossible to measure directly. Due to format restrictions, the full observer will not be presented here, as a complete estimation must be coupled with a secondary observer that recovers information about the initial velocity of the beam. This information cannot be assumed to be known generally, but is taken as a given for the preliminary developments in this paper.
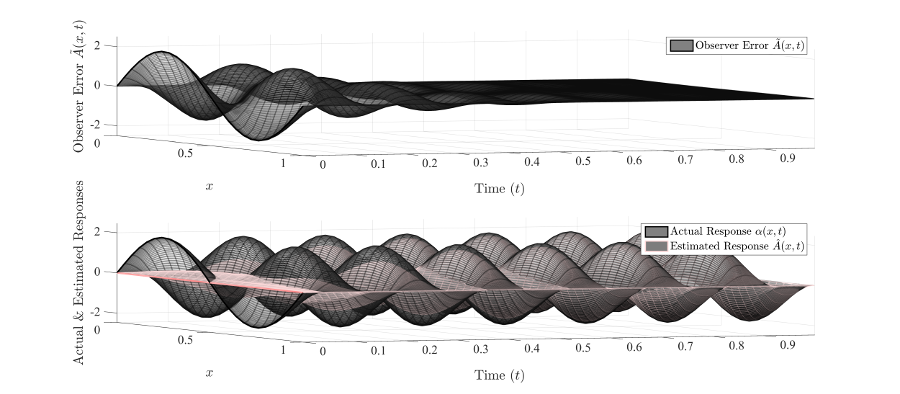
Observer error (top) and comparison between observer estimates and actual beam position (bottom)
• Dimitri Karagiannis and Verica Radisavljevic-Gajic. Robust Boundary Control for an Euler Bernoulli Beam Subject to Unknown Harmonic Disturbances with a Focus on Resonance. In Dynamic Systems and Control Conference (DSCC), pp. V003T32A009; 10 pages, Tyson’s Corner, Virginia, USA, 2017. ISBN: 978-0-7918-5829-5. doi:10.1115/DSCC2017-5264.
★★★ 2017 Best Vibrations Paper Award ★★★
ABSTRACT: In this paper, a sliding mode backstepping controller for a pinned-pinned Euler-Bernoulli beam is briefly reviewed and its efficacy in the presence of unknown bounded harmonic disturbances at arbitrary frequencies is analyzed. A brief discussion of the open-loop unstable response to harmonic excitations at resonant frequencies is provided. Motivated by this, particular attention is given to excitations at the natural frequencies of the system. It is shown that in the face of such resonant disturbances, the sliding mode backstepping controller is able to eliminate the vibrations in the beam system where backstepping control alone cannot. Indeed it is shown that if the disturbances are not accounted for, the closed loop system exhibits large (relative to the initial conditions) steady state harmonic vibrations. When the unknown resonant harmonic disturbances are accounted for via the sliding mode backstepping technique, the steady state position is constant and does not exhibit any vibrations, and furthermore it reaches this steady state exponentially at an arbitrarily selected rate.
2017 Best Vibrations Paper awarded by the ASME DSCD Technical Committee on Vibrations. Pictured left to right: Drs. Dumitru Caruntu (Vibrations TC Chair), Verica Radisavljevic-Gajic, Dimitri Karagiannis
• Dimitri Karagiannis, Verica Radisavljevic-Gajic, and Hashem Ashrafiuon. Control of Human Immunodeficiency Virus (HIV) Dynamics with Parameter Uncertainties. In Dynamic Systems and Control Conference (DSCC), page V001T09A003; 10 pages, Minneapolis, Minnesota, USA, 2016. ISBN 978-0-7918-5069-5. doi: 10.1115/DSCC2016-9755
ABSTRACT: This work considers a 3-state nonlinear model with two inputs for the controlled dynamics of the human immunodeficiency virus (HIV). The three states represent the number of healthy and unhealthy T-cells as well as the number of free virus particles in a person’s body. The two inputs represent two different types of antiretrovial drugs that are available to treat a person infected with the virus. These inputs can be used to create a stable nominal point that is much healthier for the patient than the open-loop stable equilibrium point. The goal of this paper is to use the inputs, which are subject to constraints, to efficiently and accurately reach the desired nominal point despite parameter uncertainties. We have designed an integral sliding mode control law to achieve this goal, and simulations are presented to demonstrate the performance of the controller.
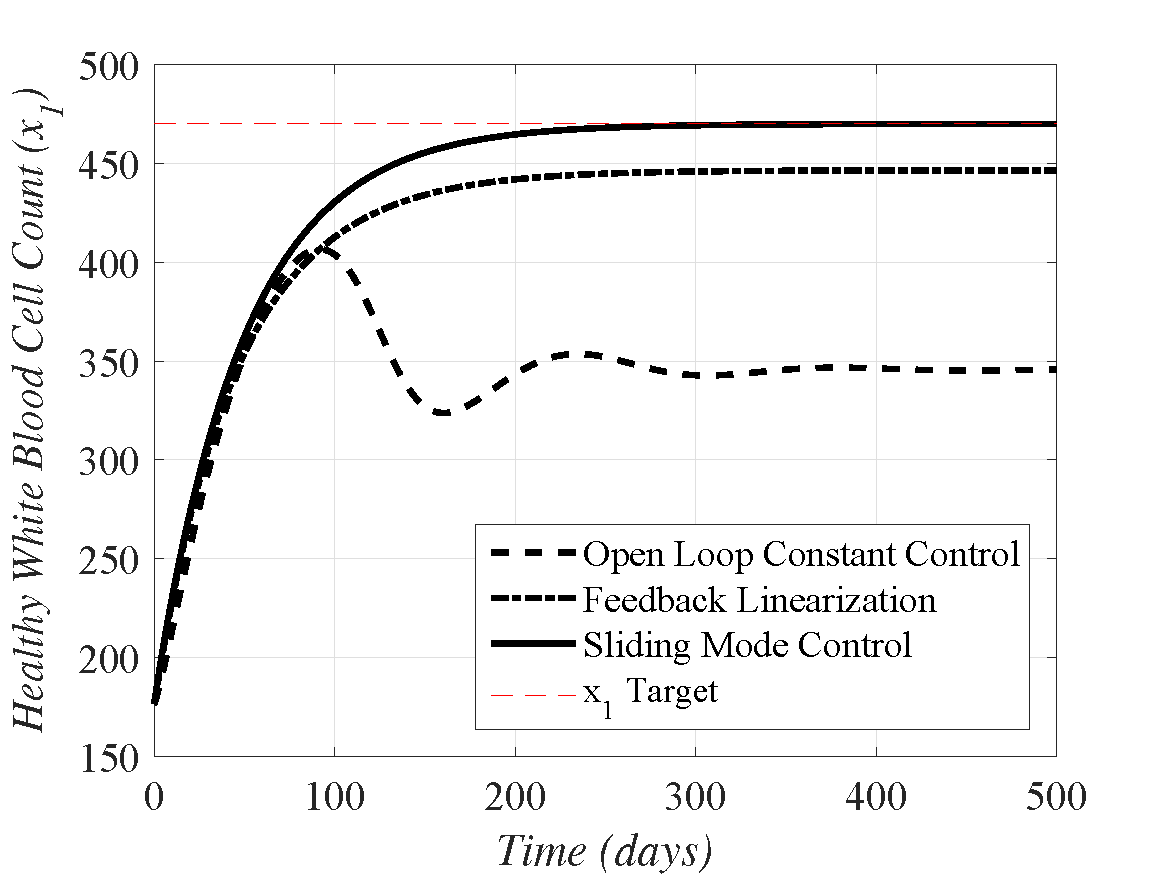Steady state healthy white blood cell comparison using robust vs. non-robust techniques
• Verica Radisavljevic-Gajic, Dimitrios A Karagiannis, Meng-Bi Cheng, and Wu-Chung Su. Recent trends in stabilization and control of distributed parameter dynamic systems. In International Mechanical Engineering Congress and Expositions (IMECE), page V04AT04A004; 8 pages, Montreal, Quebec, Canada, 2014. ISBN 978-0-7918-4647-6. doi: 10.1115/IMECE2014-37151.
ABSTRACT: The field of control and stabilization of distributed parameter systems described by partial differential equations has recently seen an increasing number of results published by very respected researchers in excellent control engineering and applied mathematics journals. This paper presents a survey of control and stabilization results with emphasis on controls. Various distributed parameter dynamic control and stabilization problems have been studied corresponding to heat conduction, wave propagation, Schrodinger equation, crowd (swarm) dynamics, magneto-hydro-dynamic channel flow, string and beam equations, viscous Burger equation, and general diffusion equations. Various techniques have been used for control and stabilization of such systems: Lyapunov stabilization, backstepping, gain scheduling, singular perturbations, sliding mode control, observer driven controller, tracking control, sampled-data control, neural networks. The field still remains widely open for future research. Applications of surveyed results to various areas including robots, aircraft, networks, transmission lines, electrochemical processes in energy systems are indicated.
• Dimitri Karagiannis and Verica Radisavljevic-Gajic. Sliding mode boundary control for an euler-bernoulli beam with boundary disturbances and parameter variations. In American Control Conference (ACC), pages 4536-4542, Portland, Oregon, USA, 2014. doi: 10.1109/ACC.2014.6859052.
ABSTRACT: This work addresses the problem of stability and control of an Euler-Bernoulli beam with sliding-pinned boundary conditions. The control comes in the form of an applied displacement and bending moment on the pinned end. The proposed controller accounts for bounded exogenous disturbances on the pinned end boundary conditions, representing a number of possible practical issues such as model parameter uncertainties or unknown external forces. This controller takes advantage of a technique for stabilizing an Euler-Bernoulli beam through a Schrodinger equation representation and a previously developed integral transformation which provides the opportunity to select arbitrary damping for the system. The contribution of this work is to introduce unknown boundary disturbances into the system boundary terms and the development of a Sliding Mode Controller which effectively drives the system states to an exponentially stable infinite-dimensional sliding surface which then eliminates the system vibration with arbitrary damping. The resulting control efforts developed are continuous functions and therefore do not create a chattering effect on control actuators.
Dimitri Karagiannis, Ph.D., Engineering, Temple University